Два цилиндра (48.40) — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
 
(не показано 10 промежуточных версий 3 участников)
Строка 1: Строка 1:
 
'''Задача 48.40 из сборника задач Мещерского:''' составить уравнения движения двух цилиндров и смоделировать систему на языке программирования JavaScript.
 
'''Задача 48.40 из сборника задач Мещерского:''' составить уравнения движения двух цилиндров и смоделировать систему на языке программирования JavaScript.
 +
[[File:4840.png|thumb|right]]
 
==Формулировка задачи==
 
==Формулировка задачи==
 
Шероховатый цилиндр массы m и радиуса r катится без скольжения по внутренней поверхности полого цилиндра массы M и радиуса R, могущего вращаться около своей горизонтально расположенной оси O. Моменты инерции цилиндров относительно своих осей равны <math>\frac{1}{2}\  mr ^{2}</math> и <math>MR^{2}</math>. Составить уравнения движения системы.
 
Шероховатый цилиндр массы m и радиуса r катится без скольжения по внутренней поверхности полого цилиндра массы M и радиуса R, могущего вращаться около своей горизонтально расположенной оси O. Моменты инерции цилиндров относительно своих осей равны <math>\frac{1}{2}\  mr ^{2}</math> и <math>MR^{2}</math>. Составить уравнения движения системы.
 
==Решение задачи==
 
==Решение задачи==
 +
Используем уравнение Лагранжа 2-го рода:
 +
 
<math>\frac{d}{dt}\left(\frac{\partial L}{\partial\dot q_i}\right) - \frac{\partial L}{\partial q_i} = 0  ,  (i = 1,2)</math> , где
 
<math>\frac{d}{dt}\left(\frac{\partial L}{\partial\dot q_i}\right) - \frac{\partial L}{\partial q_i} = 0  ,  (i = 1,2)</math> , где
 
  L = T - П - функция Лагранжа
 
  L = T - П - функция Лагранжа
Строка 9: Строка 12:
 
  q - независимые обобщенные координаты
 
  q - независимые обобщенные координаты
  
−
В данной задаче в качестве обобщенных координат примем углы φ и ψ <math>\varphi </math>.
+
В данной задаче в качестве обобщенных координат примем углы <math>\varphi </math> и <math>\psi </math>.
  
 
Представим:
 
Представим:
−
<math>T = T_1+T_2</math>, где <math>T_1</math> - кинетическая энергия цилиндра массы M, а <math>Т_2</math> - цилиндра массы m
+
 
 +
<math>T = T_1+T_2</math>, где <math>T_1</math> - кинетическая энергия цилиндра массы M, а <math>Т_2</math> - цилиндра массы m.
 +
 
 
Полый цилиндр массы M вращается вокруг неподвижной оси, следовательно:
 
Полый цилиндр массы M вращается вокруг неподвижной оси, следовательно:
 +
 
<math>T_1 = \frac{1}{2}MR^{2}\dot ψ</math>
 
<math>T_1 = \frac{1}{2}MR^{2}\dot ψ</math>
 +
 
Движение цилиндра массы m плоское.
 
Движение цилиндра массы m плоское.
−
<math>T_2 = \frac{1}{2}mV^{2}+\frac{1}{2}I_2 ω^{2}</math>
+
 
 +
<math>T_2 = \frac{1}{2}mV^{2}+\frac{1}{4}mr^{2} ω^{2}</math>
 +
 
 +
Где <math>V</math> - скорость центра масс цилиндра массой m(точки O<sub>1</sub>):
 +
 
 +
<math>V = \dot φ (R-r)</math>
 +
 
 +
Обозначим θ - угол поворота цилиндра массы m относительно точки O<sub>1</sub>, а ω - угловая скорость вращения относительно этой точки:
 +
 
 +
<math>θr = φ(R-r)-ψR</math>
 +
 
 +
<math>ω = \dot θ = \frac{R-r}{r}\dot φ - \frac{R}{r}\dot ψ</math>
 +
 
 +
Окончательно получаем T и П(определяется только силой тяжести цилиндра массой m):
 +
 
 +
<math>T = \frac{1}{2}MR^{2}\dot ψ + \frac{1}{4}m(3(R-r)^{2}\dot φ^{2}-2R(R-r)\dot φ\dot ψ + (R\dot ψ)^{2})</math>
 +
 
 +
<math>П = mg(R-r)(1-cosφ)</math>
 +
 
 +
Таким образом,
 +
 
 +
<math>L = \frac{1}{2}MR^{2}\dot ψ + \frac{1}{4}m(3(R-r)^{2}\dot φ^{2}-2R(R-r)\dot φ\dot ψ + (R\dot ψ)^{2}) - mg(R-r)(1-cosφ) </math>
 +
 
 +
Найдем:
 +
 
 +
<math>\frac{\partial L}{\partial\dot ψ} = MR^{2}\dot ψ + \frac{1}{2}mR(R\dot ψ - (R-r)\dot φ)</math>
 +
 
 +
<math>\frac{\partial L}{\partial ψ} = 0 </math>
 +
 
 +
<math>\frac{d}{dt}\left(\frac{\partial L}{\partial\dot ψ}\right) = MR^{2}\ddot ψ + \frac{1}{2}mR(R\ddot ψ - (R-r)\ddot φ)</math>
 +
 
 +
<math>\frac{\partial L}{\partial\dot φ} = \frac{3}{2}m(R-r)^{2}\dot φ - \frac{1}{2}mR(R-r)\dot ψ</math>
 +
 
 +
<math>\frac{\partial L}{\partial φ} = -mg(R-r)sinφ </math>
 +
 
 +
<math>\frac{d}{dt}\left(\frac{\partial L}{\partial\dot φ}\right) = \frac{3}{2}m(R-r)^{2}\ddot φ - \frac{1}{2}mR(R-r)\ddot ψ</math>
 +
 
 +
В результате получаем уравнения, описывающие движение рассматриваемой системы:
 +
 
 +
<math>MR^{2}\ddot ψ + \frac{1}{2}mR(R\ddot ψ - (R-r)\ddot φ) = 0</math>
 +
 
 +
<math>\frac{3}{2}(R-r)\ddot φ - \frac{1}{2}R\ddot ψ + gsinφ = 0</math>
 +
 
 +
или:
 +
 
 +
<math>\ddot ψ - \frac{m^{2}(R-r)}{2M(M+m)R}\ddot φ</math>
 +
 
 +
<math>\ddot φ - \frac{R}{3(R-r)}\ddot ψ + \frac{2g}{3(R-r)}sinφ</math>
 +
 
 
==Реализация на языке JavaScript==
 
==Реализация на языке JavaScript==
 
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Barsukov/4840.html|width=750 |height=550|border=0 }}
 
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Barsukov/4840.html|width=750 |height=550|border=0 }}
 +
 +
<div class="mw-collapsible mw-collapsed">
 +
'''Текст программы на языке JavaScript:'''
 +
<div class="mw-collapsible-content">
 +
Файл '''"4840.html"'''
 +
<syntaxhighlight lang="javascript" line start="1" enclose="div">
 +
 +
<!DOCTYPE html>
 +
 +
<html>
 +
 +
<head>
 +
    <title>4840</title>
 +
    <script type="text/javascript" src="http://tm.spbstu.ru/htmlets/Barsukov\three.js"></script>
 +
    <script type="text/javascript" src="http://tm.spbstu.ru/htmlets/Barsukov\jquery-1.9.0.js"></script>
 +
    <script type="text/javascript" src="http://tm.spbstu.ru/htmlets/Barsukov\stats.js"></script>
 +
    <script type="text/javascript" src="http://tm.spbstu.ru/htmlets/Barsukov\dat.gui.js"></script>
 +
<script type="text/javascript" src="http://tm.spbstu.ru/htmlets/Barsukov\OrbitControls.js"></script>
 +
    <style>
 +
        body{
 +
            /* set margin to 0 and overflow to hidden, to go fullscreen */
 +
            margin: 0;
 +
            overflow: hidden;
 +
        }
 +
    </style>
 +
</head>
 +
<body>
 +
 +
<div id="Stats-output"></div>
 +
<div id="WebGL-output"></div>
 +
 +
<script type="text/javascript">
 +
 +
    $(function () {
 +
var stats = initStats();
 +
 +
        var scene = new THREE.Scene();
 +
 +
        var camera = new THREE.PerspectiveCamera(45, window.innerWidth / window.innerHeight, 0.1, 1000);
 +
 +
        var renderer = new THREE.WebGLRenderer();
 +
 +
        renderer.setClearColor(new THREE.Color(0xEEEEEE, 1.0));
 +
        renderer.setSize(window.innerWidth, window.innerHeight);
 +
        renderer.shadowMapEnabled = true;
 +
 +
var axes = new THREE.AxisHelper( 20 );
 +
axes.position.x = -40;
 +
axes.position.z = 20;
 +
                scene.add(axes);
 +
 +
var spotLight = new THREE.SpotLight( 0xffffff );
 +
spotLight.position.set( -100, 0, -10 );
 +
scene.add(spotLight );
 +
 +
var cylinder = createMesh(new THREE.CylinderGeometry(20, 20, 20,30,1,true));
 +
                scene.add(cylinder);
 +
 +
var cylinder1 = createMesh1(new THREE.CylinderGeometry(5, 5, 20, 30, 1));
 +
                cylinder1.position.x=0;
 +
                cylinder1.position.y=0;
 +
                cylinder1.position.z=-15;
 +
                scene.add(cylinder1);
 +
 +
var group1 = new THREE.Object3D();
 +
group1.add(cylinder);
 +
group1.add(cylinder1);
 +
group1.position.x = 0;
 +
group1.position.y = -10;
 +
scene.add(group1);
 +
 +
        function createMesh(geom) {
 +
            var meshMaterial = new THREE.MeshNormalMaterial();
 +
            meshMaterial.side = THREE.DoubleSide;
 +
            var wireFrameMat = new THREE.MeshBasicMaterial();
 +
            wireFrameMat.wireframe = true;
 +
            var mesh = THREE.SceneUtils.createMultiMaterialObject(geom, [meshMaterial, wireFrameMat]);
 +
            return mesh;
 +
 +
        }
 +
function createMesh1(geom) {
 +
var texture = THREE.ImageUtils.loadTexture("http://tm.spbstu.ru/htmlets/Barsukov\bathroom.jpg")
 +
                        var mat = new THREE.MeshPhongMaterial();
 +
                        mat.map = texture;
 +
var mesh = new THREE.Mesh(geom, mat);
 +
return mesh;
 +
        }
 +
 +
        camera.position.x = 0;
 +
        camera.position.y = -150;
 +
        camera.position.z = 100;
 +
        camera.lookAt(scene.position);
 +
 +
$("#WebGL-output").append(renderer.domElement);
 +
renderer.render(scene, camera);
 +
var stats = initStats();
 +
cameraControls = new THREE.OrbitControls(camera, renderer.domElement);
 +
cameraControls.maxDistance = 100;
 +
cameraControls.minDistance = 0.5;
 +
cameraControls.update();
 +
 +
        var controls = new function() {
 +
            this.Speed = 0.05;
 +
            this.Rotation = 0.01;
 +
            this.M1 = 0.2;
 +
            this.M2 = 0.05;
 +
    this.phi = '0';
 +
        }
 +
 +
        var gui = new dat.GUI();
 +
        gui.add(controls, 'Speed',0,0.1);
 +
        gui.add(controls, 'Rotation',0,0.1);
 +
        gui.add(controls, 'M1',0.2,0.5);
 +
        gui.add(controls, 'M2',0.01,0.05);
 +
gui.add(controls,'phi').listen()
 +
render();
 +
 +
var step = 0;
 +
var psi2 = 0;
 +
var phi = Math.PI/2;
 +
var psi = 0;
 +
var phi2 = 0;
 +
var phi1 = 0;
 +
var psi1 = 0;
 +
function render() {
 +
stats.update();
 +
cameraControls.update();
 +
requestAnimationFrame(render);
 +
renderer.render(scene, camera);
 +
step += controls.Speed;
 +
psi2 = (0.375*controls.M2*controls.M2)/(controls.M1*(controls.M1+controls.M2));
 +
phi2 = 0.44*psi2 - 0.44*Math.sin(phi);
 +
psi1 = psi1+psi2*controls.Speed;
 +
phi1 = phi1+phi2*controls.Speed;
 +
phi = phi+phi1*controls.Speed;
 +
psi = psi+psi1*controls.Speed;
 +
w = 3*phi1-4*psi1;
 +
controls.phi=phi;
 +
cylinder1.rotation.y = 4*w;
 +
cylinder.rotation.y = w+Math.PI/2;
 +
cylinder1.position.x=15*Math.sin(phi);
 +
cylinder1.position.z=-15*Math.abs((Math.cos(phi)));
 +
group1.rotation.z += controls.Rotation;
 +
}
 +
 +
function initStats() {
 +
                    var stats = new Stats();
 +
                    stats.setMode(0); // 0: fps, 1: ms
 +
                    stats.domElement.style.position = 'absolute';
 +
                    stats.domElement.style.left = '0px';
 +
                    stats.domElement.style.top = '0px';
 +
                    $("#Stats-output").append(stats.domElement);
 +
                    return stats;
 +
        }
 +
    });
 +
 +
</script>
 +
</body>
 +
</html>
 +
 +
</syntaxhighlight>
 +
</div>
 +
</div>

Текущая версия на 21:07, 17 декабря 2017

Задача 48.40 из сборника задач Мещерского: составить уравнения движения двух цилиндров и смоделировать систему на языке программирования JavaScript.

4840.png

Формулировка задачи[править]

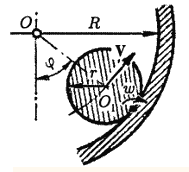
Шероховатый цилиндр массы m и радиуса r катится без скольжения по внутренней поверхности полого цилиндра массы M и радиуса R, могущего вращаться около своей горизонтально расположенной оси O. Моменты инерции цилиндров относительно своих осей равны [math]\frac{1}{2}\ mr ^{2}[/math] и [math]MR^{2}[/math]. Составить уравнения движения системы.

Решение задачи[править]

Используем уравнение Лагранжа 2-го рода:

[math]\frac{d}{dt}\left(\frac{\partial L}{\partial\dot q_i}\right) - \frac{\partial L}{\partial q_i} = 0 , (i = 1,2)[/math] , где 

L = T - П - функция Лагранжа
T - кинетическая энергия системы
П - потенциальная энергия системы
q - независимые обобщенные координаты

В данной задаче в качестве обобщенных координат примем углы [math]\varphi [/math] и [math]\psi [/math].

Представим:

[math]T = T_1+T_2[/math], где [math]T_1[/math] - кинетическая энергия цилиндра массы M, а [math]Т_2[/math] - цилиндра массы m.

Полый цилиндр массы M вращается вокруг неподвижной оси, следовательно:

[math]T_1 = \frac{1}{2}MR^{2}\dot ψ[/math]

Движение цилиндра массы m плоское.

[math]T_2 = \frac{1}{2}mV^{2}+\frac{1}{4}mr^{2} ω^{2}[/math]

Где [math]V[/math] - скорость центра масс цилиндра массой m(точки O1):

[math]V = \dot φ (R-r)[/math]

Обозначим θ - угол поворота цилиндра массы m относительно точки O1, а ω - угловая скорость вращения относительно этой точки:

[math]θr = φ(R-r)-ψR[/math]

[math]ω = \dot θ = \frac{R-r}{r}\dot φ - \frac{R}{r}\dot ψ[/math]

Окончательно получаем T и П(определяется только силой тяжести цилиндра массой m):

[math]T = \frac{1}{2}MR^{2}\dot ψ + \frac{1}{4}m(3(R-r)^{2}\dot φ^{2}-2R(R-r)\dot φ\dot ψ + (R\dot ψ)^{2})[/math]

[math]П = mg(R-r)(1-cosφ)[/math]

Таким образом,

[math]L = \frac{1}{2}MR^{2}\dot ψ + \frac{1}{4}m(3(R-r)^{2}\dot φ^{2}-2R(R-r)\dot φ\dot ψ + (R\dot ψ)^{2}) - mg(R-r)(1-cosφ) [/math]

Найдем:

[math]\frac{\partial L}{\partial\dot ψ} = MR^{2}\dot ψ + \frac{1}{2}mR(R\dot ψ - (R-r)\dot φ)[/math]

[math]\frac{\partial L}{\partial ψ} = 0 [/math]

[math]\frac{d}{dt}\left(\frac{\partial L}{\partial\dot ψ}\right) = MR^{2}\ddot ψ + \frac{1}{2}mR(R\ddot ψ - (R-r)\ddot φ)[/math]

[math]\frac{\partial L}{\partial\dot φ} = \frac{3}{2}m(R-r)^{2}\dot φ - \frac{1}{2}mR(R-r)\dot ψ[/math]

[math]\frac{\partial L}{\partial φ} = -mg(R-r)sinφ [/math]

[math]\frac{d}{dt}\left(\frac{\partial L}{\partial\dot φ}\right) = \frac{3}{2}m(R-r)^{2}\ddot φ - \frac{1}{2}mR(R-r)\ddot ψ[/math]

В результате получаем уравнения, описывающие движение рассматриваемой системы:

[math]MR^{2}\ddot ψ + \frac{1}{2}mR(R\ddot ψ - (R-r)\ddot φ) = 0[/math]

[math]\frac{3}{2}(R-r)\ddot φ - \frac{1}{2}R\ddot ψ + gsinφ = 0[/math]

или:

[math]\ddot ψ - \frac{m^{2}(R-r)}{2M(M+m)R}\ddot φ[/math]

[math]\ddot φ - \frac{R}{3(R-r)}\ddot ψ + \frac{2g}{3(R-r)}sinφ[/math]

Реализация на языке JavaScript[править]

Текст программы на языке JavaScript:

Файл "4840.html" 

  1 <!DOCTYPE html>
  2 
  3 <html>
  4 
  5 <head>
  6     <title>4840</title>
  7     <script type="text/javascript" src="http://tm.spbstu.ru/htmlets/Barsukov\three.js"></script>
  8     <script type="text/javascript" src="http://tm.spbstu.ru/htmlets/Barsukov\jquery-1.9.0.js"></script>
  9     <script type="text/javascript" src="http://tm.spbstu.ru/htmlets/Barsukov\stats.js"></script>
 10     <script type="text/javascript" src="http://tm.spbstu.ru/htmlets/Barsukov\dat.gui.js"></script>
 11 	<script type="text/javascript" src="http://tm.spbstu.ru/htmlets/Barsukov\OrbitControls.js"></script>
 12     <style>
 13         body{
 14             /* set margin to 0 and overflow to hidden, to go fullscreen */
 15             margin: 0;
 16             overflow: hidden;
 17         }
 18     </style>
 19 </head>
 20 <body>
 21 
 22 <div id="Stats-output"></div>
 23 <div id="WebGL-output"></div>
 24 
 25 <script type="text/javascript">
 26 
 27     $(function () {
 28 		var stats = initStats();
 29 
 30         var scene = new THREE.Scene();
 31 
 32         var camera = new THREE.PerspectiveCamera(45, window.innerWidth / window.innerHeight, 0.1, 1000);
 33 
 34         var renderer = new THREE.WebGLRenderer();
 35 
 36         renderer.setClearColor(new THREE.Color(0xEEEEEE, 1.0));
 37         renderer.setSize(window.innerWidth, window.innerHeight);
 38         renderer.shadowMapEnabled = true;
 39 		
 40 		var axes = new THREE.AxisHelper( 20 );
 41 		axes.position.x = -40;
 42 		axes.position.z = 20;
 43                 scene.add(axes);
 44 		
 45 		var spotLight = new THREE.SpotLight( 0xffffff );
 46 		spotLight.position.set( -100, 0, -10 );
 47 		scene.add(spotLight );
 48 		
 49 		var cylinder = createMesh(new THREE.CylinderGeometry(20, 20, 20,30,1,true));
 50                 scene.add(cylinder);
 51 		
 52 		var cylinder1 = createMesh1(new THREE.CylinderGeometry(5, 5, 20, 30, 1));
 53                 cylinder1.position.x=0;
 54                 cylinder1.position.y=0;
 55                 cylinder1.position.z=-15;
 56                 scene.add(cylinder1);
 57 		
 58 		var group1 = new THREE.Object3D();
 59 		group1.add(cylinder);
 60 		group1.add(cylinder1);
 61 		group1.position.x = 0;
 62 		group1.position.y = -10;
 63 		scene.add(group1);
 64 		
 65         function createMesh(geom) {
 66             var meshMaterial = new THREE.MeshNormalMaterial();
 67             meshMaterial.side = THREE.DoubleSide;
 68             var wireFrameMat = new THREE.MeshBasicMaterial();
 69             wireFrameMat.wireframe = true;
 70             var mesh = THREE.SceneUtils.createMultiMaterialObject(geom, [meshMaterial, wireFrameMat]);
 71             return mesh;
 72 			
 73         }
 74 		function createMesh1(geom) {
 75 			var texture = THREE.ImageUtils.loadTexture("http://tm.spbstu.ru/htmlets/Barsukov\bathroom.jpg")
 76                         var mat = new THREE.MeshPhongMaterial();
 77                         mat.map = texture;			
 78 			var mesh = new THREE.Mesh(geom, mat);			
 79 			return mesh;
 80         }
 81 
 82         camera.position.x = 0;
 83         camera.position.y = -150;
 84         camera.position.z = 100;
 85         camera.lookAt(scene.position);
 86 
 87 		$("#WebGL-output").append(renderer.domElement);
 88 		renderer.render(scene, camera);
 89 		var stats = initStats();
 90 		cameraControls = new THREE.OrbitControls(camera, renderer.domElement);
 91 		cameraControls.maxDistance = 100;
 92 		cameraControls.minDistance = 0.5;
 93 		cameraControls.update();
 94 		
 95         var controls = new function() {
 96             this.Speed = 0.05;
 97             this.Rotation = 0.01;
 98             this.M1 = 0.2;
 99             this.M2 = 0.05;
100 	    this.phi = '0';
101         }
102 
103         var gui = new dat.GUI();
104         gui.add(controls, 'Speed',0,0.1);
105         gui.add(controls, 'Rotation',0,0.1);
106         gui.add(controls, 'M1',0.2,0.5);
107         gui.add(controls, 'M2',0.01,0.05);
108 	gui.add(controls,'phi').listen()	
109 	render();
110 		
111 		var step = 0;
112 		var psi2 = 0;
113 		var phi = Math.PI/2;
114 		var psi = 0;
115 		var phi2 = 0;
116 		var phi1 = 0;
117 		var psi1 = 0;
118 		function render() {
119 			stats.update();
120 			cameraControls.update();
121 			requestAnimationFrame(render);
122 			renderer.render(scene, camera);
123 			step += controls.Speed;
124 			psi2 = (0.375*controls.M2*controls.M2)/(controls.M1*(controls.M1+controls.M2));
125 			phi2 = 0.44*psi2 - 0.44*Math.sin(phi);
126 			psi1 = psi1+psi2*controls.Speed;
127 			phi1 = phi1+phi2*controls.Speed;
128 			phi = phi+phi1*controls.Speed;
129 			psi = psi+psi1*controls.Speed;		
130 			w = 3*phi1-4*psi1;
131 			controls.phi=phi;
132 			cylinder1.rotation.y = 4*w;
133 			cylinder.rotation.y = w+Math.PI/2;
134 			cylinder1.position.x=15*Math.sin(phi);
135 			cylinder1.position.z=-15*Math.abs((Math.cos(phi)));
136 			group1.rotation.z += controls.Rotation;
137 		}
138 		
139 		function initStats() {
140                     var stats = new Stats();
141                     stats.setMode(0); // 0: fps, 1: ms
142                     stats.domElement.style.position = 'absolute';
143                     stats.domElement.style.left = '0px';
144                     stats.domElement.style.top = '0px';
145                     $("#Stats-output").append(stats.domElement);
146                     return stats;
147         }
148     });
149 
150 </script>
151 </body>
152 </html>
Источник — «http://tm.spbstu.ru/?title=Два_цилиндра_(48.40)&oldid=49119»