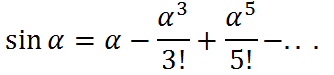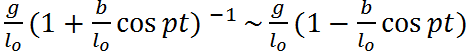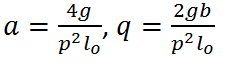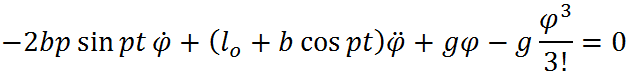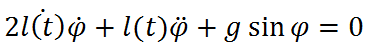Исследование колебаний математического маятника переменной длины — различия между версиями
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 48: | Строка 48: | ||
==Список литературы== | ==Список литературы== | ||
| − | + | ||
| + | 1. http://trudymai.ru/upload/iblock/459/issledovanie-rezonansnykh-kolebaniy-matematicheskogo-mayatnika-peremennoy-dliny.pdf<br /> | ||
| + | 2. http://cyberleninka.ru/article/n/upravlenie-dvizheniyami-parametricheskogo-mayatnika | ||
| + | |||
==Курсовой проект== | ==Курсовой проект== | ||
| − | [[:File:fluctuations.rar | Скачать]] | + | Программа: [[:File:fluctuations.rar | Скачать]]<br /> |
| + | Текст курсового проекта: [[:File:Исследование колебаний математического маятника переменной длины.docx | Скачать]] | ||
== Участники проекта == | == Участники проекта == | ||
Текущая версия на 17:37, 2 июня 2017
Содержание
Цель[править]
Целью нашей работы является исследование колебания маятника, длина которого меняется по гармоническому закону.
Задачи[править]
- Построить графики колебаний, используя численные методы;
- Построить фазовые портеры;
- Исследовать влияние параметров в уравнении колебаний на вид колебаний и фазовых портретов;
- Сравнить решение исходного и линеаризованного уравнения.
- Визуализировать модель маятника при помощи языка программирования JavaScript
Вывод формул[править]
Выясним, каким будет уравнение колебаний нашего маятника.
Для этого найдем кинетическую и потенциальную энергию маятника:
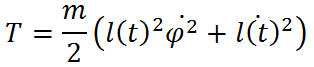
и запишем уравнение Лагранжа второго рода:
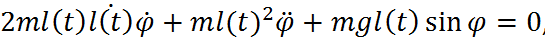
Для исследования поведения нашего маятника рассмотрим несколько случаев. Для начала рассмотрим случай пренебрежения изменения длины маятника, учитывая, что начальный угол отклонения много меньше 1 радиана.
Разложим синус в ряд Тейлора:
Ограничиваясь первым членом в разложении, получим:
Учитывая малость параметра b, заменим выражение эквивалентным:
Cведем наше уравнение к уравнению Матье: 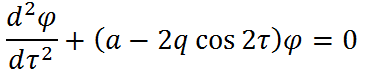
Зоны устойчивости и неустойчивости уравнения Матье представлены на диаграмме Айнса-Стретта:

Усложним задачу и учтём изменение длины маятника. Рассмотрим три варианта:
В первом приближении:
С учётом третьего порядка приближения в разложении синуса :
И исходное уравнение:
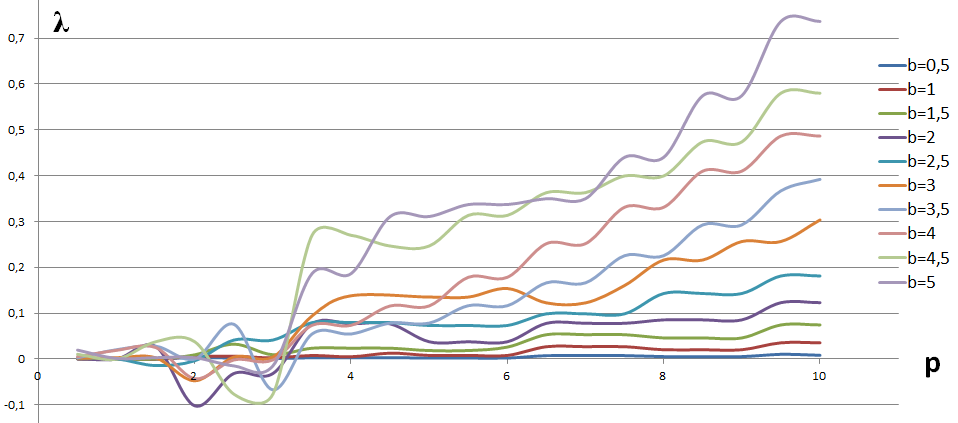
При исследовании поведения системы мы построили график зависимости скорости затухания (раскачивания) от параметров b и p. При фиксированном значении параметра b и переменном значении параметра р мы считали декремент затухания:
Из этого графика видно, что при малых значениях параметра b для p на промежутке от 1,5 до 3 декремент отрицателен. Это означает, что колебания неустойчивы и происходит раскачивание системы. При больших b видно, что с увеличением p скорость затухания увеличивается, и при фиксированном p с увеличением b скорость затухания тоже увеличивается.
Визуализация[править]
Выводы[править]
В ходе исследований колебаний математического маятника переменной длины мы рассмотрели графики колебаний и фазовые портреты. Выяснили, что при фиксировании параметра b с увеличением частоты колебания затухают быстрее, аналогичная зависимость наблюдается при фиксировании частоты и увеличении параметра b. Однако есть области раскачки колебаний. Пренебрегая изменением длины, колебания схожи с классическим маятником для устойчивого случая. Но учитывая изменение длины и беря больше членов в разложении синуса, график заметно изменяется.
Список литературы[править]
1. http://trudymai.ru/upload/iblock/459/issledovanie-rezonansnykh-kolebaniy-matematicheskogo-mayatnika-peremennoy-dliny.pdf
2. http://cyberleninka.ru/article/n/upravlenie-dvizheniyami-parametricheskogo-mayatnika
Курсовой проект[править]
Программа: Скачать
Текст курсового проекта: Скачать