Нелинейные колебания груза с вынуждающей силой — различия между версиями
Paul (обсуждение | вклад) |
|||
| (не показано 7 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | [[en:Driven oscillations of a mass on a nonlinear spring]] | ||
[[Файл:Nolinekoleban2.png|thumb|Нелинейный колебания груза с вынуждающей силой|500px]] | [[Файл:Nolinekoleban2.png|thumb|Нелинейный колебания груза с вынуждающей силой|500px]] | ||
| Строка 19: | Строка 20: | ||
Уравнение движения имеет вид: | Уравнение движения имеет вид: | ||
| − | <math>m\ddot x = -kx -{k_1}x^3 | + | <math>m\ddot x = -kx -{k_1}x^3 + {F_0}sin(t) - B \dot x</math> |
== Визуализация на языке JavaScript == | == Визуализация на языке JavaScript == | ||
| − | + | ||
| + | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Kiselev/Spring/Springs.html |width=800 |height=800 |border=0 }} | ||
| + | |||
Скачать программу: [[Медиа:SpringNoLine.rar|SpringNoLine.rar]] | Скачать программу: [[Медиа:SpringNoLine.rar|SpringNoLine.rar]] | ||
| + | |||
| + | '''Текст программы на языке JavaScript (разработчик [[Киселев Павел]]):''' <div class="mw-collapsible-content"> | ||
| + | Файл '''"Spring.js"''' | ||
| + | <syntaxhighlight lang="javascript" enclose="div"> | ||
| + | |||
| + | window.addEventListener("load", Main_Spring, true); | ||
| + | function Main_Spring() { | ||
| + | var canvas = spring_canvas; | ||
| + | canvas.onselectstart = function () {return false;}; // запрет выделения canvas | ||
| + | var ctx = canvas.getContext("2d"); // на ctx происходит рисование | ||
| + | var w = canvas.width; // ширина окна в расчетных координатах | ||
| + | var h = canvas.height; // высота окна в расчетных координатах | ||
| + | var Pi = 3.1415926; // число "пи" | ||
| + | var m0 = 1; // масштаб массы | ||
| + | var T0 = 1; // масштаб времени (период колебаний исходной системы) | ||
| + | var t = 0; | ||
| + | var k0 = 2 * Pi / T0; // масштаб частоты | ||
| + | var C0 = m0 * k0 * k0; // масштаб жесткости | ||
| + | var B0 = 2 * m0 * k0; // масштаб вязкости | ||
| + | var omega = 10; | ||
| + | |||
| + | // *** Задание физических параметров *** | ||
| + | var F = 80; | ||
| + | var m = 1 * m0; // масса | ||
| + | var C = 1 * C0; // жесткость | ||
| + | var C1 = 1 * C0; // жесткость1 | ||
| + | var B = .1 * B0; // вязкость | ||
| + | |||
| + | slider_m.value = (m / m0).toFixed(1); number_m.value = (m / m0).toFixed(1); | ||
| + | slider_C.value = (C / C0).toFixed(1); number_C.value = (C / C0).toFixed(1); | ||
| + | slider_C1.value = (C / C0).toFixed(1); number_C1.value = (C / C0).toFixed(1); | ||
| + | slider_B.value = (B / B0).toFixed(1); number_B.value = (B / B0).toFixed(1); | ||
| + | slider_F.value = (F / 40).toFixed(1); number_F.value = (F / 40).toFixed(1); | ||
| + | |||
| + | // *** Задание вычислительных параметров *** | ||
| + | |||
| + | var fps = 300; // frames per second - число кадров в секунду (качечтво отображения) | ||
| + | var spf = 100; // steps per frame - число шагов интегрирования между кадрами | ||
| + | var dt = 0.05 * T0 / fps; // шаг интегрирования (качество расчета) | ||
| + | var steps = 0; // количество шагов интегрирования | ||
| + | |||
| + | function setM(new_m) {m = new_m * m0;} | ||
| + | function setC(new_C) {C = new_C * C0;} | ||
| + | function setC1(new_C1) {C1 = new_C1 * C0 * 0.067;} | ||
| + | function setB(new_B) {B = new_B * B0;} | ||
| + | function setF(new_F) {F = new_F * 40;} | ||
| + | |||
| + | slider_m.oninput = function() {number_m.value = slider_m.value; setM(slider_m.value);}; | ||
| + | number_m.oninput = function() {slider_m.value = number_m.value; setM(number_m.value);}; | ||
| + | slider_C.oninput = function() {number_C.value = slider_C.value; setC(slider_C.value);}; | ||
| + | number_C.oninput = function() {slider_C.value = number_C.value; setC(number_C.value);}; | ||
| + | slider_C1.oninput = function() {number_C1.value = slider_C1.value; setC1(slider_C1.value);}; | ||
| + | number_C1.oninput = function() {slider_C1.value = number_C1.value; setC1(number_C1.value);}; | ||
| + | slider_B.oninput = function() {number_B.value = slider_B.value; setB(slider_B.value);}; | ||
| + | number_B.oninput = function() {slider_B.value = number_B.value; setB(number_B.value);}; | ||
| + | slider_F.oninput = function() {number_F.value = slider_F.value; setF(slider_F.value);}; | ||
| + | number_F.oninput = function() {slider_F.value = number_F.value; setF(number_F.value);}; | ||
| + | |||
| + | var count = true; // проводить ли расчет системы | ||
| + | var v = 0; // скорость тела | ||
| + | |||
| + | var rw = canvas.width / 30; | ||
| + | var rh = canvas.height / 1.5; | ||
| + | var x0 = 15 * rw - rw / 2; | ||
| + | var y0 = rh / 1.33 - rh / 2; | ||
| + | |||
| + | // параметры пружины | ||
| + | var coil = 10; // количество витков | ||
| + | var startX = 0; // закрепление пружины | ||
| + | |||
| + | // создаем прямоугольник-грузик | ||
| + | var rect = { | ||
| + | x: x0, width: rw, | ||
| + | y: y0, height: rh, | ||
| + | fill: "rgba(0, 0, 255, 1)" // цвет | ||
| + | }; | ||
| + | |||
| + | // захват прямоугольника мышью | ||
| + | var mx_; // буфер позиции мыши (для расчета скорости при отпускании шара) | ||
| + | document.onmousedown = function(e) { // функция при нажатии клавиши мыши | ||
| + | var m = mouseCoords(e); // получаем расчетные координаты курсора мыши | ||
| + | |||
| + | var x = rect.x; | ||
| + | var xw = rect.x + rect.width; | ||
| + | var y = rect.y; | ||
| + | var yh = rect.y + rect.height; | ||
| + | if (x <= m.x && xw >= m.x && y <= m.y && yh >= m.y) { | ||
| + | if (e.which == 1) { // нажата левая клавиша мыши | ||
| + | rect.xPlus = rect.x - m.x; // сдвиг курсора относительно грузика по x | ||
| + | rect.yPlus = rect.y - m.y; // сдвиг курсора относительно грузика по y | ||
| + | mx_ = m.x; | ||
| + | count = false; | ||
| + | document.onmousemove = mouseMove; // пока клавиша нажата - работает функция перемещения | ||
| + | } | ||
| + | } | ||
| + | }; | ||
| + | |||
| + | document.onmouseup = function(e) { // функция при отпускании клавиши мыши | ||
| + | document.onmousemove = null; // когда клавиша отпущена - функции перемещения нету | ||
| + | count = true; | ||
| + | }; | ||
| + | |||
| + | function mouseMove(e) { // функция при перемещении мыши, работает только с зажатой ЛКМ | ||
| + | var m = mouseCoords(e); // получаем расчетные координаты курсора мыши | ||
| + | rect.x = m.x + rect.xPlus; | ||
| + | // v = 6.0 * (m.x - mx_) / dt / fps; // сохранение инерции | ||
| + | v = 0; | ||
| + | mx_ = m.x; | ||
| + | } | ||
| + | |||
| + | function mouseCoords(e) { // функция возвращает расчетные координаты курсора мыши | ||
| + | var m = []; | ||
| + | var rect = canvas.getBoundingClientRect(); | ||
| + | m.x = (e.clientX - rect.left); | ||
| + | m.y = (e.clientY - rect.top); | ||
| + | return m; | ||
| + | } | ||
| + | |||
| + | // график | ||
| + | var vGraph = new TM_graph( // определить график | ||
| + | "#vGraph", // на html-элементе #vGraph | ||
| + | 250, // сколько шагов по оси "x" отображается | ||
| + | -1, 1, 0.2); // мин. значение оси Y, макс. значение оси Y, шаг по оси Y | ||
| + | |||
| + | function control() { | ||
| + | calculate(); | ||
| + | draw(); | ||
| + | requestAnimationFrame(control); | ||
| + | } | ||
| + | control(); | ||
| + | // setInterval(control, 1000 / fps); // Запуск системы | ||
| + | |||
| + | function calculate() { | ||
| + | if (!count) return; | ||
| + | for (var s=1; s<=spf; s++) { | ||
| + | var f = -B*v - C * (rect.x - x0) - C1*Math.pow(rect.x - x0,3)+2*F*Math.sin(t); | ||
| + | v += f / m * dt; | ||
| + | //console.log(f); | ||
| + | rect.x += v * dt; | ||
| + | t+= dt; | ||
| + | steps++; | ||
| + | if (steps % 80 == 0) vGraph.graphIter(steps, (rect.x-x0)/canvas.width*2); // подать данные на график | ||
| + | } | ||
| + | |||
| + | } | ||
| + | |||
| + | function draw() { | ||
| + | ctx.clearRect(0, 0, w, h); | ||
| + | draw_spring(startX, rect.x, h/2, 10, 50); | ||
| + | ctx.fillStyle = "#0000ff"; | ||
| + | ctx.fillRect(rect.x, rect.y, rect.width, rect.height); | ||
| + | } | ||
| + | |||
| + | |||
| + | function draw_spring(x_start, x_end, y, n, h) { | ||
| + | ctx.lineWidth = 2; | ||
| + | ctx.strokeStyle = "#7394cb"; | ||
| + | var L = x_end - x_start; | ||
| + | for (var i = 0; i < n; i++) { | ||
| + | var x_st = x_start + L / n * i; | ||
| + | var x_end = x_start + L / n * (i + 1); | ||
| + | var l = x_end - x_st; | ||
| + | ctx.beginPath(); | ||
| + | ctx.bezierCurveTo(x_st, y, x_st + l / 4, y + h, x_st + l / 2, y); | ||
| + | ctx.bezierCurveTo(x_st + l / 2, y, x_st + 3 * l / 4, y - h, x_st + l, y); | ||
| + | ctx.stroke(); | ||
| + | } | ||
| + | } | ||
| + | } | ||
Текущая версия на 18:35, 18 января 2017
Содержание
Аннотация к проекту[править]
В данном проекте изучается нелинейные колебания груза с действующей на него периодической силой
Постановка задачи[править]
Пусть подвешенный на нелинейной пружине груз массой m испытывает действие внешней силы F, которая изменяется по закону F = sin (t)
- написать программу на языке JavaScript, моделирующую поведение груза при задании различных параметров системы.
Общие сведения по теме[править]
Если на колебательную систему действует периодически изменяющаяся внешняя сила, то система совершает колебания, характер которых в той или иной мере повторяет характер изменения этой силы. Такие колебания называются вынужденными.
F0 называется амплитудой силы и является наибольшим значением силы.
| Благодаря работе, выполняемой внешней силой, увеличиваются максимальные значения, которых достигают потенциальная энергия пружины и кинетическая энергия груза. При этом будут возрастать потери на преодоление сил сопротивления. Наконец наступит момент, когда работа внешней силы станет точно компенсировать потери энергии в системе. Дальнейшее нарастание колебаний в системе прекратится, и установятся колебания с некоторой постоянной амплитудой. |
Уравнение движения имеет вид:
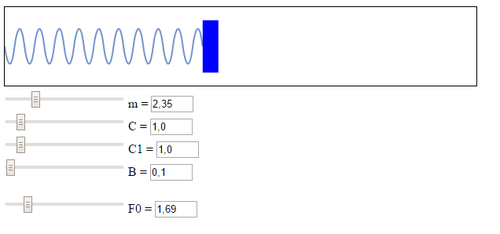
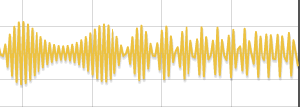
Визуализация на языке JavaScript[править]
Скачать программу: SpringNoLine.rar
Текст программы на языке JavaScript (разработчик Киселев Павел):Файл "Spring.js" <syntaxhighlight lang="javascript" enclose="div">
window.addEventListener("load", Main_Spring, true);
function Main_Spring() {
var canvas = spring_canvas;
canvas.onselectstart = function () {return false;}; // запрет выделения canvas
var ctx = canvas.getContext("2d"); // на ctx происходит рисование
var w = canvas.width; // ширина окна в расчетных координатах
var h = canvas.height; // высота окна в расчетных координатах
var Pi = 3.1415926; // число "пи"
var m0 = 1; // масштаб массы
var T0 = 1; // масштаб времени (период колебаний исходной системы)
var t = 0;
var k0 = 2 * Pi / T0; // масштаб частоты
var C0 = m0 * k0 * k0; // масштаб жесткости
var B0 = 2 * m0 * k0; // масштаб вязкости
var omega = 10;
// *** Задание физических параметров ***
var F = 80;
var m = 1 * m0; // масса
var C = 1 * C0; // жесткость
var C1 = 1 * C0; // жесткость1
var B = .1 * B0; // вязкость
slider_m.value = (m / m0).toFixed(1); number_m.value = (m / m0).toFixed(1);
slider_C.value = (C / C0).toFixed(1); number_C.value = (C / C0).toFixed(1);
slider_C1.value = (C / C0).toFixed(1); number_C1.value = (C / C0).toFixed(1);
slider_B.value = (B / B0).toFixed(1); number_B.value = (B / B0).toFixed(1);
slider_F.value = (F / 40).toFixed(1); number_F.value = (F / 40).toFixed(1);
// *** Задание вычислительных параметров ***
var fps = 300; // frames per second - число кадров в секунду (качечтво отображения) var spf = 100; // steps per frame - число шагов интегрирования между кадрами var dt = 0.05 * T0 / fps; // шаг интегрирования (качество расчета) var steps = 0; // количество шагов интегрирования
function setM(new_m) {m = new_m * m0;}
function setC(new_C) {C = new_C * C0;}
function setC1(new_C1) {C1 = new_C1 * C0 * 0.067;}
function setB(new_B) {B = new_B * B0;}
function setF(new_F) {F = new_F * 40;}
slider_m.oninput = function() {number_m.value = slider_m.value; setM(slider_m.value);};
number_m.oninput = function() {slider_m.value = number_m.value; setM(number_m.value);};
slider_C.oninput = function() {number_C.value = slider_C.value; setC(slider_C.value);};
number_C.oninput = function() {slider_C.value = number_C.value; setC(number_C.value);};
slider_C1.oninput = function() {number_C1.value = slider_C1.value; setC1(slider_C1.value);};
number_C1.oninput = function() {slider_C1.value = number_C1.value; setC1(number_C1.value);};
slider_B.oninput = function() {number_B.value = slider_B.value; setB(slider_B.value);};
number_B.oninput = function() {slider_B.value = number_B.value; setB(number_B.value);};
slider_F.oninput = function() {number_F.value = slider_F.value; setF(slider_F.value);};
number_F.oninput = function() {slider_F.value = number_F.value; setF(number_F.value);};
var count = true; // проводить ли расчет системы var v = 0; // скорость тела
var rw = canvas.width / 30; var rh = canvas.height / 1.5; var x0 = 15 * rw - rw / 2; var y0 = rh / 1.33 - rh / 2;
// параметры пружины var coil = 10; // количество витков var startX = 0; // закрепление пружины
// создаем прямоугольник-грузик
var rect = {
x: x0, width: rw,
y: y0, height: rh,
fill: "rgba(0, 0, 255, 1)" // цвет
};
// захват прямоугольника мышью
var mx_; // буфер позиции мыши (для расчета скорости при отпускании шара)
document.onmousedown = function(e) { // функция при нажатии клавиши мыши
var m = mouseCoords(e); // получаем расчетные координаты курсора мыши
var x = rect.x;
var xw = rect.x + rect.width;
var y = rect.y;
var yh = rect.y + rect.height;
if (x <= m.x && xw >= m.x && y <= m.y && yh >= m.y) {
if (e.which == 1) { // нажата левая клавиша мыши
rect.xPlus = rect.x - m.x; // сдвиг курсора относительно грузика по x
rect.yPlus = rect.y - m.y; // сдвиг курсора относительно грузика по y
mx_ = m.x;
count = false;
document.onmousemove = mouseMove; // пока клавиша нажата - работает функция перемещения
}
}
};
document.onmouseup = function(e) { // функция при отпускании клавиши мыши
document.onmousemove = null; // когда клавиша отпущена - функции перемещения нету
count = true;
};
function mouseMove(e) { // функция при перемещении мыши, работает только с зажатой ЛКМ
var m = mouseCoords(e); // получаем расчетные координаты курсора мыши
rect.x = m.x + rect.xPlus;
// v = 6.0 * (m.x - mx_) / dt / fps; // сохранение инерции
v = 0;
mx_ = m.x;
}
function mouseCoords(e) { // функция возвращает расчетные координаты курсора мыши
var m = [];
var rect = canvas.getBoundingClientRect();
m.x = (e.clientX - rect.left);
m.y = (e.clientY - rect.top);
return m;
}
// график
var vGraph = new TM_graph( // определить график
"#vGraph", // на html-элементе #vGraph
250, // сколько шагов по оси "x" отображается
-1, 1, 0.2); // мин. значение оси Y, макс. значение оси Y, шаг по оси Y
function control() {
calculate();
draw();
requestAnimationFrame(control);
}
control();
// setInterval(control, 1000 / fps); // Запуск системы
function calculate() {
if (!count) return;
for (var s=1; s<=spf; s++) {
var f = -B*v - C * (rect.x - x0) - C1*Math.pow(rect.x - x0,3)+2*F*Math.sin(t);
v += f / m * dt; //console.log(f);
rect.x += v * dt;
t+= dt;
steps++;
if (steps % 80 == 0) vGraph.graphIter(steps, (rect.x-x0)/canvas.width*2); // подать данные на график
}
}
function draw() {
ctx.clearRect(0, 0, w, h);
draw_spring(startX, rect.x, h/2, 10, 50);
ctx.fillStyle = "#0000ff";
ctx.fillRect(rect.x, rect.y, rect.width, rect.height);
}
function draw_spring(x_start, x_end, y, n, h) {
ctx.lineWidth = 2;
ctx.strokeStyle = "#7394cb";
var L = x_end - x_start; for (var i = 0; i < n; i++) { var x_st = x_start + L / n * i; var x_end = x_start + L / n * (i + 1); var l = x_end - x_st; ctx.beginPath(); ctx.bezierCurveTo(x_st, y, x_st + l / 4, y + h, x_st + l / 2, y); ctx.bezierCurveTo(x_st + l / 2, y, x_st + 3 * l / 4, y - h, x_st + l, y); ctx.stroke(); } }
}