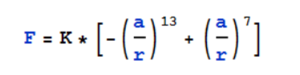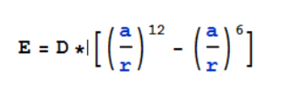13632/1 Потенциал Леннард-Джонса — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
| (не показано 6 промежуточных версий 2 участников) | |||
| Строка 2: | Строка 2: | ||
==Джон Эдвард Леннард-Джонс== | ==Джон Эдвард Леннард-Джонс== | ||
Английский физик. (1894-1954) | Английский физик. (1894-1954) | ||
| − | |||
==Определение потенциала Леннард-Джонса== | ==Определение потенциала Леннард-Джонса== | ||
| − | Потенциал Леннард-Джонса описывает энергию взаимодействия между двумя атомами в инертном газе одноатомного типа. | + | Потенциал Леннард-Джонса описывает энергию взаимодействия между двумя атомами в инертном газе одноатомного типа.[[File:fghj.png|75 px|right]] |
| − | |||
==Уравнения потенциала== | ==Уравнения потенциала== | ||
Между двумя атомами идеального газа существует сила равная: | Между двумя атомами идеального газа существует сила равная: | ||
*[[File:f1.PNG|300 px|left]] *[[File:fo2.PNG|250 px]]<br /> | *[[File:f1.PNG|300 px|left]] *[[File:fo2.PNG|250 px]]<br /> | ||
где D — энергия связи, a — длина связи.<br /><br /> | где D — энергия связи, a — длина связи.<br /><br /> | ||
| − | Для примера возьмём r - расстояние между атомами. Силой трения мы пренебрегаем.Энергия между этими двумя атомами находится из такого дифференциального уравнения: | + | Для примера возьмём r - расстояние между атомами. Силой трения мы пренебрегаем.Энергия между этими двумя атомами находится из такого дифференциального уравнения(1): |
[[File:fo4.PNG|300 px|left]]<br /><br /> | [[File:fo4.PNG|300 px|left]]<br /><br /> | ||
где D и a - константы<br /><br /><br /> | где D и a - константы<br /><br /><br /> | ||
| − | + | '''График, отражающий зависимость энергии от расстояния:'''<br /> | |
| − | '''График, отражающий зависимость энергии от расстояния:''' | ||
[[File:F14.PNG|400 px|left]]<br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /> | [[File:F14.PNG|400 px|left]]<br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /> | ||
| − | Решив численным методом дифференциальное уравнение (1), построим '''график решения с помощью матлаб:''' | + | Решив численным методом дифференциальное уравнение (1), построим '''график решения с помощью матлаб:'''<br /> |
| − | + | [[File:vtime.jpg|400 px]] <br /> | |
| − | + | Если учесть, что силы трения пропорциональны скорости [[File:fo6.PNG|170 px]] сила станет равна:[[File:fo7.PNG|350 px]] | |
| − | Если учесть, что силы трения пропорциональны скорости [[File:fo6.PNG| | + | отсюда '''график r(t):'''<br />[[File:r(t)2.png|450 px]]<br /> |
| − | отсюда график r(t): | + | '''Скорости относительно времени v(t):'''<br />[[File:v(t).png|400 px]]<br /> |
| − | [[File: | ||
==Вывод из уравнений(графики):== | ==Вывод из уравнений(графики):== | ||
| − | Скорости относительно расстояния между атомами v(r): | + | '''Скорости относительно расстояния между атомами v(r): '''<br /> |
| − | [[File:f12.PNG|400 px|left]] | + | [[File:f12.PNG|400 px|left]]<br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /><br /> |
| + | '''Сила взаимодействия относительно расстояния между атомами F(r):'''<br /> | ||
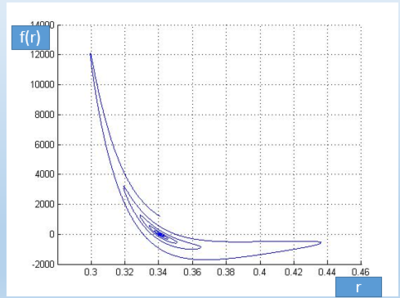
| + | [[File:f13.PNG|400 px]] | ||
Текущая версия на 23:38, 15 января 2017
Содержание
Джон Эдвард Леннард-Джонс[править]
Английский физик. (1894-1954)
Определение потенциала Леннард-Джонса[править]
Потенциал Леннард-Джонса описывает энергию взаимодействия между двумя атомами в инертном газе одноатомного типа.
Уравнения потенциала[править]
Между двумя атомами идеального газа существует сила равная:
- *
где D — энергия связи, a — длина связи.
Для примера возьмём r - расстояние между атомами. Силой трения мы пренебрегаем.Энергия между этими двумя атомами находится из такого дифференциального уравнения(1):
где D и a - константы
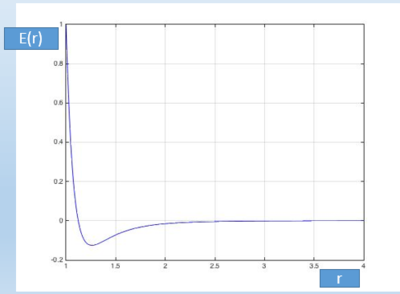
График, отражающий зависимость энергии от расстояния:
Решив численным методом дифференциальное уравнение (1), построим график решения с помощью матлаб:
Если учесть, что силы трения пропорциональны скорости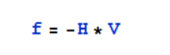 
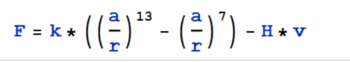
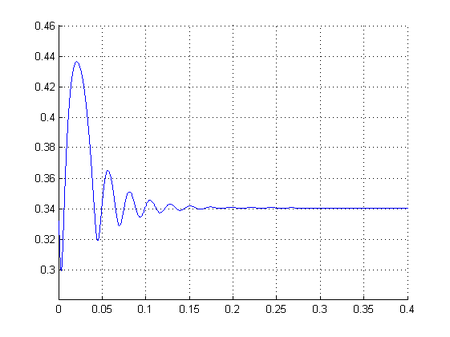
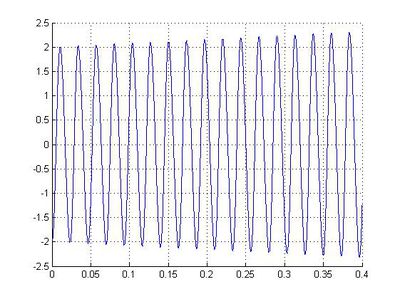
сила станет равна:
отсюда график r(t):2.png)
Скорости относительно времени v(t):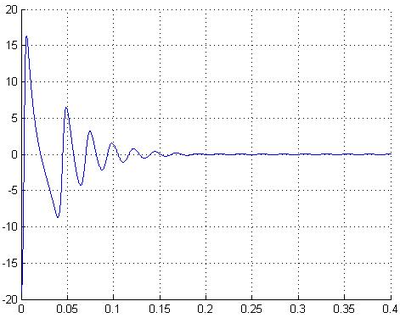.png)
Вывод из уравнений(графики):[править]
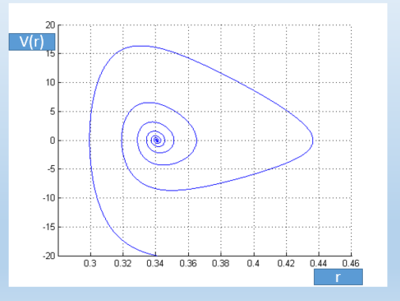
Скорости относительно расстояния между атомами v(r):
Сила взаимодействия относительно расстояния между атомами F(r):
