"Уравнение Мещерского" — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
Catvicaf (обсуждение | вклад) (Новая страница: «right ==Задание характеристик системы== *Движение происходит с постоянным…») |
(→Вывод формулы) |
||
| Строка 8: | Строка 8: | ||
==Вывод формулы== | ==Вывод формулы== | ||
В момент времени t + Δt импульс ракеты равен (M - ∆M)(v+ ∆v) а импульс испущенных газов равен ∆ M(u+v). В момент времени t импульс всей системы был равен Mv. Предполагая систему «ракета + газы» замкнутой, можно записать: | В момент времени t + Δt импульс ракеты равен (M - ∆M)(v+ ∆v) а импульс испущенных газов равен ∆ M(u+v). В момент времени t импульс всей системы был равен Mv. Предполагая систему «ракета + газы» замкнутой, можно записать: | ||
| − | [[File:Vvvvnnnn.png|thumbnail| | + | [[File:Vvvvnnnn.png|thumbnail|center]] |
==Зависимость массы ракеты и топлива от скорости== | ==Зависимость массы ракеты и топлива от скорости== | ||
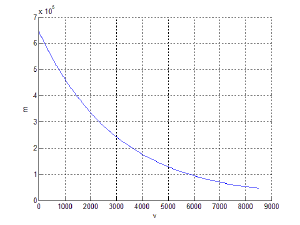
[[File:Vvvvnnn.bmp|thumbnail|right]] | [[File:Vvvvnnn.bmp|thumbnail|right]] | ||
Проанализировав входные данные, получили , что при уменьшении массы ракеты и топлива скорость ракеты увеличивается. | Проанализировав входные данные, получили , что при уменьшении массы ракеты и топлива скорость ракеты увеличивается. | ||
Текущая версия на 19:34, 22 декабря 2016
Задание характеристик системы[править]
- Движение происходит с постоянным ускорением, и описывается уравнением Мещерского;
- Рассматривается горизонтальное движение в космосе;
- Присутствует внешняя сила F;
Вывод формулы[править]
В момент времени t + Δt импульс ракеты равен (M - ∆M)(v+ ∆v) а импульс испущенных газов равен ∆ M(u+v). В момент времени t импульс всей системы был равен Mv. Предполагая систему «ракета + газы» замкнутой, можно записать:
Зависимость массы ракеты и топлива от скорости[править]
Проанализировав входные данные, получили , что при уменьшении массы ракеты и топлива скорость ракеты увеличивается.