Колебания материальной точки в поле силы тяжести — различия между версиями
(содержание) |
|||
| (не показано 25 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
[[Виртуальная лаборатория]] > [[Колебания материальной точки в поле силы тяжести]] <HR> | [[Виртуальная лаборатория]] > [[Колебания материальной точки в поле силы тяжести]] <HR> | ||
| − | == Краткое описание == | + | == Краткое описание системы == |
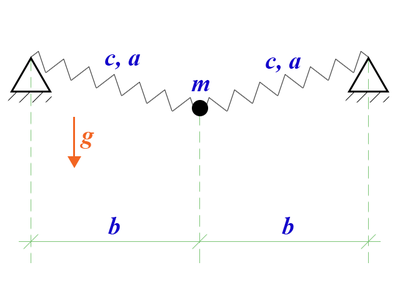
| − | + | Рассмотрим механическую систему с двумя степенями свободы: материальная точка массы <math>m</math> связана пружинами с двумя опорами, вся система находится в поле силы тяжести. Расстояние между опорами <math>2b</math>, длина пружин в недеформированном состоянии <math>a</math>, жесткость пружин <math>c</math>. | |
| + | [[File:Scheme l.png|400px|left|Схема]] | ||
| + | Обозначим: | ||
| + | ::<math> | ||
| + | S^{+} = \sqrt{y^{2}+(a+x)^{2}}\\ | ||
| + | S^{-} = \sqrt{y^{2}+(a-x)^{2}}\\ | ||
| + | </math> | ||
| + | Уравнения движения системы будут выглядеть так: | ||
| + | ::<math> | ||
| + | \left\{ | ||
| + | \begin{array}{ll} | ||
| + | m \ddot{x} = \frac {c(a+x)}{S^{+}}(a-S^{+})-\frac {c(a-x)}{S^{+}}(a-S^{-})\\ | ||
| + | \displaystyle m \ddot{y} = -\frac {cy}{S^{+}}(a-S^{+})-\frac {cy}{S^{+}}(a-S^{-})+mg\\ | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| − | + | ==Реализация== | |
| + | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Lobas/yiiis.html |width=1250 |height=1650 |border=0 }} | ||
| + | <br /> | ||
| − | + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | |
| + | '''Текст программы на языке JavaScript:''' <div class="mw-collapsible-content"> | ||
| + | function MainBall(canvas, canvasX, canvasY) { | ||
| − | |||
| − | + | var context = canvas.getContext("2d"); //основная картинка | |
| + | var contextX = canvasX.getContext("2d"); //график отклонения по Х | ||
| + | var contextY = canvasY.getContext("2d"); //график отклонения по У | ||
| + | |||
| + | var Pi = 3.1415926; //число пи | ||
| − | + | var m0 = 1; //масштаб массы | |
| + | var T0 = 1; //масштаб времени | ||
| + | var a0 = 1; //масштаб расстояния | ||
| − | + | var k0 = 2 * Pi / T0; //масштаб частоты | |
| + | var C0 = m0 * k0 * k0; //масштаб жесткости | ||
| − | + | var m = 1 * m0; //масса | |
| + | var r = 5 * a0; //визуальный радиус шарика | ||
| + | var C = 0.3 * C0; //жесткость пружин | ||
| + | var l = 100 * a0; //длина пружин | ||
| + | var g = 9.80665 * a0 / T0 / T0; //ускорение свободного падения | ||
| + | var t = 0 * T0; //начальное время | ||
| + | |||
| + | var fps = 50; //кадры в секунду | ||
| + | var spf = 5; //кол-во шагов интегрирования на один кадр | ||
| + | var dt = 0.4 * T0 / fps; //шаг интегрирования | ||
| + | |||
| + | |||
| + | var h = canvas.height; //высота картинки | ||
| + | var w = canvas.width; //ширина картинки | ||
| + | var hScale = canvas.height / l; //коэффициент пересчета по высоте | ||
| + | var wScale = canvas.width / l; //коэффициент пересчета по ширине | ||
| + | |||
| + | var ball = {'x':0, 'y':0, 'vx':0, 'vy':0, 'ax':0, 'ay':0}; //НУ | ||
| + | var sqp = 0; //корень со знаком + | ||
| + | var sqm = 0; //корень со знаком - | ||
| + | var n1 = 0; //переменные для считывания команд пользователя | ||
| + | var n2 = 0; | ||
| + | var n3 = 0; | ||
| + | var n4 = 0; | ||
| + | var ab = 1; | ||
| + | var gr = 0; | ||
| + | MainBall.prototype.setXo = function(n1){ball.x = n1;}; //считывание координаты Х | ||
| + | MainBall.prototype.setYo = function(n2){ball.y = n2;}; //считывание координаты У | ||
| + | MainBall.prototype.setVXo = function(n3){ball.vx = ball.vx * n3;}; //обнуление скорости по Х | ||
| + | MainBall.prototype.setVYo = function(n4){ball.vy = ball.vy * n4;}; //обнуление скорости по У | ||
| + | MainBall.prototype.setAB = function(n5){ab = n5;}; //считывание отношения а/b | ||
| + | |||
| + | number_ab.oninput = function() {MainBall.prototype.setAB(Number(number_ab.value));} | ||
| + | |||
| + | restart.onclick = function(){ | ||
| + | ball.x = 0; | ||
| + | ball.y = 0; | ||
| + | ball.vx = input_vx.value * 50; | ||
| + | ball.vy = input_vy.value * 50; | ||
| + | } | ||
| + | |||
| + | function control() { | ||
| + | physics(); | ||
| + | draw(); | ||
| + | } | ||
| + | //вычисления | ||
| + | function physics(){ | ||
| + | for (var s=1; s<=spf; s++) { | ||
| + | sqm = Math.sqrt(ball.y * ball.y + (l - ball.x) * (l - ball.x)); //вычисление корня со знаком - | ||
| + | sqp = Math.sqrt(ball.y * ball.y + (l + ball.x) * (l + ball.x)); //вычисление корня со знаком + | ||
| + | ball.ax = (C * (ball.x + l) * (l * ab - sqp) / sqp - C * (l - ball.x) * (l - sqm) / sqm) / m; //вычисление ускорения по Х | ||
| + | ball.ay = (- C * ball.y * (sqp - l * ab) / sqp + C * ball.y * (l - sqm) / sqm + m * g) / m; //вычисление ускорения по У | ||
| + | ball.vx += ball.ax * dt; //вычисление скорости по Х | ||
| + | ball.vy += ball.ay * dt; //вычисление скорости по У | ||
| + | ball.x += ball.vx * dt; //вычисление координаты Х | ||
| + | ball.y += ball.vy * dt; //вычисление координаты У | ||
| + | t += dt; //приращение времени | ||
| + | /*alert(ball.x + " " + ball.y + " " + ball.vx + " " + ball.vy + " " + ball.ax + " " + ball.ay);*/ | ||
| + | |||
| + | } | ||
| + | } | ||
| + | //рисование вспомогательных элементов графиков | ||
| + | contextX.beginPath(); | ||
| + | contextX.strokeStyle = "#bbbbbb"; | ||
| + | contextX.moveTo(0, h/4); | ||
| + | contextX.lineTo(1200, h/4); | ||
| + | contextX.closePath(); | ||
| + | contextX.stroke(); | ||
| + | |||
| + | contextY.beginPath(); | ||
| + | contextY.strokeStyle = "#bbbbbb"; | ||
| + | contextY.moveTo(0, h/4); | ||
| + | contextY.lineTo(1200, h/4); | ||
| + | contextY.closePath(); | ||
| + | contextY.stroke(); | ||
| + | //рисование шарика и пружин | ||
| + | function draw(){ | ||
| + | context.fillStyle = "#00ff00"; //рисование пружин | ||
| + | context.beginPath(); | ||
| + | context.clearRect(0, 0, w, h); | ||
| + | context.moveTo(0, h / 2); | ||
| + | context.lineTo(ball.x * wScale + w / 2, ball.y * hScale + h / 2); | ||
| + | context.lineTo(w, h / 2); | ||
| + | context.stroke(); | ||
| + | context.closePath(); | ||
| + | |||
| + | context.fillStyle = "#0000ff"; //рисование шарика | ||
| + | context.beginPath(); | ||
| + | context.arc(ball.x * wScale + w / 2, ball.y * hScale + h / 2, r * wScale, 0, 2 * Pi, false); | ||
| + | context.fill(); | ||
| + | context.closePath(); | ||
| + | |||
| + | context.fillStyle = "#ff0000"; //рисование опор | ||
| + | context.beginPath(); | ||
| + | context.arc(0, h / 2, a0 * wScale, 0, 2 * Pi, false); | ||
| + | context.arc(w, h / 2, a0 * wScale, 0, 2 * Pi, false); | ||
| + | context.fill(); | ||
| + | context.closePath(); | ||
| + | |||
| + | contextX.beginPath(); //рисование графика Х | ||
| + | contextX.strokeStyle = 'black'; | ||
| + | contextX.moveTo(t*20 - dt * 10 - gr * 1200, ((ball.x - ball.vx * dt * 5) * 5 + h/2) / 2); | ||
| + | contextX.lineTo(t*20 - gr * 1200, (ball.x * 5 + h/2) / 2); | ||
| + | contextX.closePath(); | ||
| + | contextX.stroke(); | ||
| + | |||
| + | contextY.beginPath(); //рисование графика У | ||
| + | contextY.strokeStyle = 'black'; | ||
| + | contextY.moveTo(t*20 - dt * 10 - gr * 1200, ((ball.y - ball.vy * dt * 5) * 5 + h/2) / 2); | ||
| + | contextY.lineTo(t*20 - gr * 1200, (ball.y * 5 + h/2) / 2); | ||
| + | contextY.closePath(); | ||
| + | contextY.stroke(); | ||
| + | |||
| + | if (t * 20 > (gr + 1) * 1200) { | ||
| + | contextX.clearRect(0, 0, 1200, h); | ||
| + | contextY.clearRect(0, 0, 1200, h); | ||
| + | |||
| + | contextX.beginPath(); | ||
| + | contextX.strokeStyle = "#bbbbbb"; | ||
| + | contextX.moveTo(0, h/4); | ||
| + | contextX.lineTo(1200, h/4); | ||
| + | contextX.closePath(); | ||
| + | contextX.stroke(); | ||
| + | |||
| + | contextY.beginPath(); | ||
| + | contextY.strokeStyle = "#bbbbbb"; | ||
| + | contextY.moveTo(0, h/4); | ||
| + | contextY.lineTo(1200, h/4); | ||
| + | contextY.closePath(); | ||
| + | contextY.stroke(); | ||
| + | gr++; | ||
| + | }; | ||
| + | } | ||
| + | |||
| + | setInterval(control, 1000/fps); | ||
| + | } | ||
| + | </div> | ||
| + | |||
| + | ==Ссылки== | ||
| + | *Разработчик : [[Лобас Анна]] | ||
| + | * [[Виртуальная лаборатория]] | ||
| + | *[http://tm.spbstu.ru/htmlets/Lobas/YIIS.rar Скачать программу] | ||
Текущая версия на 23:14, 30 ноября 2016
Виртуальная лаборатория > Колебания материальной точки в поле силы тяжестиКраткое описание системы[править]
Рассмотрим механическую систему с двумя степенями свободы: материальная точка массы связана пружинами с двумя опорами, вся система находится в поле силы тяжести. Расстояние между опорами , длина пружин в недеформированном состоянии , жесткость пружин .
Обозначим:
Уравнения движения системы будут выглядеть так:
Реализация[править]
function MainBall(canvas, canvasX, canvasY) {
var context = canvas.getContext("2d"); //основная картинка
var contextX = canvasX.getContext("2d"); //график отклонения по Х var contextY = canvasY.getContext("2d"); //график отклонения по У
var Pi = 3.1415926; //число пи
var m0 = 1; //масштаб массы var T0 = 1; //масштаб времени var a0 = 1; //масштаб расстояния
var k0 = 2 * Pi / T0; //масштаб частоты var C0 = m0 * k0 * k0; //масштаб жесткости
var m = 1 * m0; //масса
var r = 5 * a0; //визуальный радиус шарика
var C = 0.3 * C0; //жесткость пружин
var l = 100 * a0; //длина пружин var g = 9.80665 * a0 / T0 / T0; //ускорение свободного падения var t = 0 * T0; //начальное время
var fps = 50; //кадры в секунду var spf = 5; //кол-во шагов интегрирования на один кадр var dt = 0.4 * T0 / fps; //шаг интегрирования
var h = canvas.height; //высота картинки
var w = canvas.width; //ширина картинки var hScale = canvas.height / l; //коэффициент пересчета по высоте var wScale = canvas.width / l; //коэффициент пересчета по ширине
var ball = {'x':0, 'y':0, 'vx':0, 'vy':0, 'ax':0, 'ay':0}; //НУ
var sqp = 0; //корень со знаком + var sqm = 0; //корень со знаком - var n1 = 0; //переменные для считывания команд пользователя var n2 = 0; var n3 = 0; var n4 = 0; var ab = 1; var gr = 0;
MainBall.prototype.setXo = function(n1){ball.x = n1;}; //считывание координаты Х
MainBall.prototype.setYo = function(n2){ball.y = n2;}; //считывание координаты У
MainBall.prototype.setVXo = function(n3){ball.vx = ball.vx * n3;}; //обнуление скорости по Х MainBall.prototype.setVYo = function(n4){ball.vy = ball.vy * n4;}; //обнуление скорости по У MainBall.prototype.setAB = function(n5){ab = n5;}; //считывание отношения а/b
number_ab.oninput = function() {MainBall.prototype.setAB(Number(number_ab.value));}
restart.onclick = function(){ ball.x = 0; ball.y = 0; ball.vx = input_vx.value * 50; ball.vy = input_vy.value * 50; }
function control() {
physics();
draw();
}
//вычисления
function physics(){
for (var s=1; s<=spf; s++) {
sqm = Math.sqrt(ball.y * ball.y + (l - ball.x) * (l - ball.x)); //вычисление корня со знаком - sqp = Math.sqrt(ball.y * ball.y + (l + ball.x) * (l + ball.x)); //вычисление корня со знаком +
ball.ax = (C * (ball.x + l) * (l * ab - sqp) / sqp - C * (l - ball.x) * (l - sqm) / sqm) / m; //вычисление ускорения по Х
ball.ay = (- C * ball.y * (sqp - l * ab) / sqp + C * ball.y * (l - sqm) / sqm + m * g) / m; //вычисление ускорения по У ball.vx += ball.ax * dt; //вычисление скорости по Х ball.vy += ball.ay * dt; //вычисление скорости по У ball.x += ball.vx * dt; //вычисление координаты Х ball.y += ball.vy * dt; //вычисление координаты У t += dt; //приращение времени /*alert(ball.x + " " + ball.y + " " + ball.vx + " " + ball.vy + " " + ball.ax + " " + ball.ay);*/
}
}
//рисование вспомогательных элементов графиков contextX.beginPath(); contextX.strokeStyle = "#bbbbbb"; contextX.moveTo(0, h/4); contextX.lineTo(1200, h/4); contextX.closePath(); contextX.stroke();
contextY.beginPath(); contextY.strokeStyle = "#bbbbbb"; contextY.moveTo(0, h/4); contextY.lineTo(1200, h/4); contextY.closePath(); contextY.stroke(); //рисование шарика и пружин
function draw(){
context.fillStyle = "#00ff00"; //рисование пружин
context.beginPath();
context.clearRect(0, 0, w, h);
context.moveTo(0, h / 2);
context.lineTo(ball.x * wScale + w / 2, ball.y * hScale + h / 2); context.lineTo(w, h / 2); context.stroke();
context.closePath();
context.fillStyle = "#0000ff"; //рисование шарика
context.beginPath();
context.arc(ball.x * wScale + w / 2, ball.y * hScale + h / 2, r * wScale, 0, 2 * Pi, false);
context.fill();
context.closePath();
context.fillStyle = "#ff0000"; //рисование опор
context.beginPath();
context.arc(0, h / 2, a0 * wScale, 0, 2 * Pi, false);
context.arc(w, h / 2, a0 * wScale, 0, 2 * Pi, false);
context.fill();
context.closePath();
contextX.beginPath(); //рисование графика Х contextX.strokeStyle = 'black'; contextX.moveTo(t*20 - dt * 10 - gr * 1200, ((ball.x - ball.vx * dt * 5) * 5 + h/2) / 2); contextX.lineTo(t*20 - gr * 1200, (ball.x * 5 + h/2) / 2); contextX.closePath(); contextX.stroke();
contextY.beginPath(); //рисование графика У contextY.strokeStyle = 'black'; contextY.moveTo(t*20 - dt * 10 - gr * 1200, ((ball.y - ball.vy * dt * 5) * 5 + h/2) / 2); contextY.lineTo(t*20 - gr * 1200, (ball.y * 5 + h/2) / 2); contextY.closePath(); contextY.stroke();
if (t * 20 > (gr + 1) * 1200) { contextX.clearRect(0, 0, 1200, h); contextY.clearRect(0, 0, 1200, h);
contextX.beginPath(); contextX.strokeStyle = "#bbbbbb"; contextX.moveTo(0, h/4); contextX.lineTo(1200, h/4); contextX.closePath(); contextX.stroke();
contextY.beginPath(); contextY.strokeStyle = "#bbbbbb"; contextY.moveTo(0, h/4); contextY.lineTo(1200, h/4); contextY.closePath(); contextY.stroke(); gr++; }; }
setInterval(control, 1000/fps);
}
Ссылки[править]
- Разработчик : Лобас Анна
- Виртуальная лаборатория
- Скачать программу