Механика дискретных сред и аномальные тепловые процессы — различия между версиями
| Строка 1: | Строка 1: | ||
| − | [[А.М. Кривцов: выступления]] > '''Механика дискретных сред и аномальные тепловые процессы''' <HR> | + | [[А.М. Кривцов: выступления]] > '''Механика дискретных сред и аномальные тепловые процессы.''' <HR> |
{{DISPLAYTITLE:<span style="display:none">{{FULLPAGENAME}}</span>}} | {{DISPLAYTITLE:<span style="display:none">{{FULLPAGENAME}}</span>}} | ||
| − | <font size="3">ДОКЛАД "МЕХАНИКА ДИСКРЕТНЫХ СРЕД И АНОМАЛЬНЫЕ ТЕПЛОВЫЕ ПРОЦЕССЫ"</font> | + | <font size="3">ДОКЛАД "МЕХАНИКА ДИСКРЕТНЫХ СРЕД И АНОМАЛЬНЫЕ ТЕПЛОВЫЕ ПРОЦЕССЫ."</font> |
Кривцов Антон Мирославович (СПбПУ, ИПМаш РАН) | Кривцов Антон Мирославович (СПбПУ, ИПМаш РАН) | ||
| + | == Аннотация == | ||
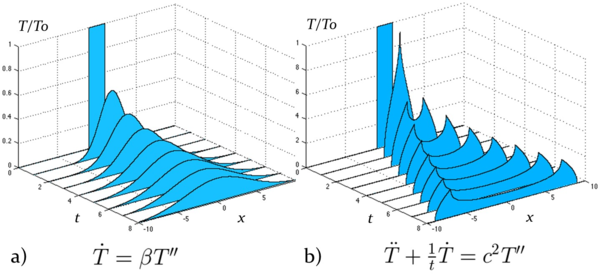
В докладе излагаются подходы и приложения механики дискретных сред. Рассматриваются задачи, в которых проявляется нарушение континуальности среды – или в силу дискретности структуры вещества, или в силу особенности протекающих в нем процессов. Подробно рассматриваются задачи, связанные с описанием аномальных тепловых процессов на микроуровне: немонотонной тепловой релаксации, тепловой сверхпроводимости и др. Предлагаются подходы, позволяющие в простейших случаях на основе уравнений динамики частиц вещества получить аналитическое описание указанных процессов. Проводится сравнение эволюции теплового возмущения при обычной теплопроводности (рис. 1а) и тепловой сверхпроводимости (рис. 1b). Показывается, что тепло в сверхпроводящих системах может распространяться со скоростью, близкой к скорости звука, что открывает возможность для перспективных практических приложений. | В докладе излагаются подходы и приложения механики дискретных сред. Рассматриваются задачи, в которых проявляется нарушение континуальности среды – или в силу дискретности структуры вещества, или в силу особенности протекающих в нем процессов. Подробно рассматриваются задачи, связанные с описанием аномальных тепловых процессов на микроуровне: немонотонной тепловой релаксации, тепловой сверхпроводимости и др. Предлагаются подходы, позволяющие в простейших случаях на основе уравнений динамики частиц вещества получить аналитическое описание указанных процессов. Проводится сравнение эволюции теплового возмущения при обычной теплопроводности (рис. 1а) и тепловой сверхпроводимости (рис. 1b). Показывается, что тепло в сверхпроводящих системах может распространяться со скоростью, близкой к скорости звука, что открывает возможность для перспективных практических приложений. | ||
| + | |||
[[Файл:Sdkhgsdghsd.png|600px|Рисунок 1. Эволюция прямоугольного теплового импульса: a) теплопроводность Фурье, b) тепловая сверхпроводимость.]] | [[Файл:Sdkhgsdghsd.png|600px|Рисунок 1. Эволюция прямоугольного теплового импульса: a) теплопроводность Фурье, b) тепловая сверхпроводимость.]] | ||
| + | |||
| + | |||
| + | == Литература == | ||
| + | [[А.М. Кривцов]]. '''Распространение тепла в бесконечном одномерном гармоническом кристалле'''. [http://www.maik.ru/cgi-perl/journal.pl?lang=rus&name=dan Доклады Академии Наук]. 2015, том 464, № 2, C. 162-166 ([[Медиа: Krivtsov_2015 DAN rus proof.pdf|pdf]], [[Распространение тепла в гармоническом одномерном кристалле|моделирование]]). English version: [[Krivtsov A. M.]] '''Heat transfer in infinite harmonic one dimensional crystals.''' [http://www.maik.rssi.ru/cgi-perl/journal.pl?name=danphys&page=main Doklady Physics], 2015, Vol. 60, No. 9, pp. 407–411. (Download pdf: [[Медиа: Krivtsov 2015 DAN eng.pdf.pdf|190 Kb]]) | ||
Версия 17:57, 6 октября 2016
А.М. Кривцов: выступления > Механика дискретных сред и аномальные тепловые процессы.
ДОКЛАД "МЕХАНИКА ДИСКРЕТНЫХ СРЕД И АНОМАЛЬНЫЕ ТЕПЛОВЫЕ ПРОЦЕССЫ."
Кривцов Антон Мирославович (СПбПУ, ИПМаш РАН)
Аннотация
В докладе излагаются подходы и приложения механики дискретных сред. Рассматриваются задачи, в которых проявляется нарушение континуальности среды – или в силу дискретности структуры вещества, или в силу особенности протекающих в нем процессов. Подробно рассматриваются задачи, связанные с описанием аномальных тепловых процессов на микроуровне: немонотонной тепловой релаксации, тепловой сверхпроводимости и др. Предлагаются подходы, позволяющие в простейших случаях на основе уравнений динамики частиц вещества получить аналитическое описание указанных процессов. Проводится сравнение эволюции теплового возмущения при обычной теплопроводности (рис. 1а) и тепловой сверхпроводимости (рис. 1b). Показывается, что тепло в сверхпроводящих системах может распространяться со скоростью, близкой к скорости звука, что открывает возможность для перспективных практических приложений.
Литература
А.М. Кривцов. Распространение тепла в бесконечном одномерном гармоническом кристалле. Доклады Академии Наук. 2015, том 464, № 2, C. 162-166 (pdf, моделирование). English version: Krivtsov A. M. Heat transfer in infinite harmonic one dimensional crystals. Doklady Physics, 2015, Vol. 60, No. 9, pp. 407–411. (Download pdf: 190 Kb)