Моделирование динамической потери устойчивости стержней — различия между версиями

Версия 11:17, 21 июня 2016

МАГИСТЕРСКАЯ РАБОТА
Автор работы: Краморов Данил
Научный руководитель: к. ф-м. н. В. А. Кузькин

Введение и мотивация работы

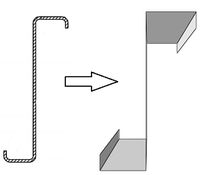
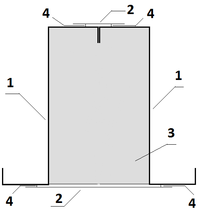
В настоящее время в мировой практике широкое распространение приобрели стержневые конструкции из оцинкованных тонкостенных холодногнутых профилей. В отличие от стальных конструкций, где установлены геометрические соотношения параметров сечения их стержневых элементов, заведомо обеспечивающие местную устойчивость, в элементах ЛСТК потеря местной устойчивости допускается на ранних стадиях нагружения. Поэтому в настоящее время одним из актуальных направлений исследования является изучение влияния потери местной устойчивости стержневых тонкостенных холодногнутых профилей.

Решаются следующие задачи:

• создание наиболее простой конечно-элементной модели стержня
• исследование статической потери устойчивости тонкостенного стержня
• исследование динамической потери устойчивости сплошного и тонкостенного стержней

Тонкостенный стержень — стержень, у которого все три основных размера (наибольший и наименьший размеры поперечного сечения и длина) являются величинами различного порядка. В отличие от обычных (сплошных) стержней, сечения тонкостенного стержня при деформации не остаются плоскими (явление депланации), что исключает возможность использования при расчёте гипотезы плоских сечений [1]. Благодаря лёгкости и экономичности, тонкостенные конструкции получили широкое распространение в строительстве. Относительно легкий вес также не ограничивает инженеров и производителей в выборе формы поперечного сечения профилей [2]. Основная часть расчетов производилась методом конечных элементов (МКЭ) в программе ABAQUS [3]. Для твердотельного построения статической потери устойчивости был выбран тип элементов 3D stress с 8 степенями свободы, для оболочечных – Shell с 4 степенями свободы. В динамическом случае – 3D wire shape с заданным сечением. Во всех постановках геометрический порядок сетки – линейный. При большом количестве элементов он дает точность близкую к квадратичному порядку, а вот скорость расчета становится выше. Материал конструкции – сталь (E=210 ГПа, ν =0.3) в упругой постановке.

Статическая форма потери устойчивости

Исследования статической потери устойчивости проводились с использованием оболочечной модели. С точки зрения МКЭ разница между твердотельной и оболочечной моделью в следующем:

• в оболочечной модели не требуется разбиение сетки по толщине стержня
• в оболочечном построении изменение толщины происходит почти мгновенно заменой данного параметра, тогда как в твердотельном приходится перестраивать весь эскиз модели

Упрощение модели

Максимальная разница между оболочеченой и твердотельной постановками – 5% в пользу оболочечной модели – позволяет использовать оболочечную модель. Отсутствие скругления же показывает разницу 6% в пользу твердотельной модели, что в комбинации с оболочечной постановкой позволяет использовать упрощенную модель практически без потери точности.

Схема модели с саморезами

Объединение стержней в составное сечение значительно повышает несущую способность стержня, позволяя использовать его в местах подверженных максимальной нагрузке (например, в колоннах). В рамках бакалаврской было доказано, что оптимальным способом объединения является объединение планками. Был получен понижающий коэффициент, позволяющий учитывать в расчете податливость саморезов. Однако были найдены ошибки в моделировании, при пересчете уже в рамках магистерской данный коэффициент увеличился с 0.85 до 0.93. То есть идеально жесткое крепление планок к профилю уменьшает точность расчета несущей способности примерно на 7%.

Тонкостенный профиль может иметь практически любое сечение, в том числе потому что форма сечения создается загибом тонкого стального листа. Но при многократном использовании станка может возникнуть дефект. Нормативно дефект производства в 1° является допустимым. Было доказано:

• отклонение в 5° при любой постановке дает максимальную погрешность в 5%
• наибольшее влияние оказывает отклонение стенки стержня от вертикали
• отклонение отгибов от прямого угла не создает существенной ошибки

Кроме того для дальнейшего упрощения в рамках данного исследования было проведено сравнение оболочечной и балочной постановки. Разница между постановками оказалась несущественной, что позволяет в дальнейшем использовать именно балочное построение.

Динамическая форма потери устойчивости

Потеря устойчивости стержней на сжатие – классическая проблема механики твердого тела. В 1744 году Леонард Эйлер предсказал критическую силу для потери устойчивости на сжатие колоны в статическом случае. Многочисленные эксперименты и теоретические исследования показывают, что в динамическом случае поведение колоны значительно усложняется. В частности, в динамике максимальная сила не равна Эйлеровой статической силе. Поведение колоны при потере устойчивости в динамическом случае зависит от способа сжатия. В данном исследовании исследуется потеря устойчивости при нагрузке с постоянной скоростью.

Модель Хоффа

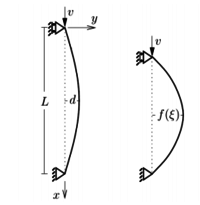
В этой главе будет решаться задача в поставке Хоффа. Хофф исследовал сжатие колоны с изначальным несовершенством в гидравлическом прессе, где два конца колоны двигались навстречу друг другу с постоянной скоростью. Продольные колебания колонны не учитывались.

Исследуя динамическую потерю устойчивости стержней, Кузькин В.А. получил формулу, которая легка в основу данного исследования:

[math]\frac{P_*}{P_e} = 1 + (frac{3}{4\Omega^{frac{1}{2}})[/math]

[math]w(x,t)=\sqrt{\frac{32}{\pi }}\frac{K_{IC}}{E^{\prime }}\sqrt{x_{\ast }-x} +O\left( (x_{\ast }-x)^{\alpha }\right) , \label{eq:opening_near_tip} [/math]

Исходя из нее максимальная сила сжатия стержня в постановке Хоффа зависит исключительно от геометрических параметров стержня и скорости сжатия. При стремлении амплитуды несовершенства к нулю (к идеальному стержню) и маленьких значениях скорости максимальная сила стремится к эйлеровой статической силе.

Аналогичный эксперимент были реализован в рамках конечно-элементной модели. За основу была взята балка с заданным круглым сечением. Длина балки – 5м, радиус сечения – 0.1м. На нижнем конце балки были запрещены перемещения, верхний конец балки мог двигаться вдоль оси приложения силы. Скорости сжатия находились в пределах от 0.15мм/с до 5 м/с. Значения несовершенства от 10-1 до 10-6.

Сравнение аналитического и конечно-элементного решения

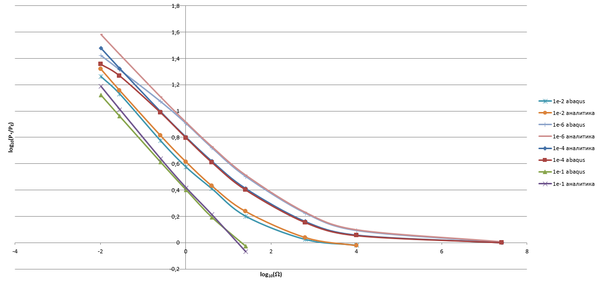
В итоге было был построен график сравнения аналитического решения и конечно-элементного моделирования. На график были нанесены значения для разных скоростей сжатия и различных амплитуд несовершенства.

Надо отметить, что при меньших значениях несовершенства Abaqus практически не показал дальнейшей разницы, что не позволяет рассмотреть корректность формулы при приближении к совершенной колоне. Минимальная амплитуда несовершенства оказалось равна значению в 10-6.

Стоит обратить внимание, что при высокой скорости сжатия КЭ моделирование также показало расхождение с аналитикой. Таким образом можно получить верхнюю границу использование формулы. Данные расчеты справедливы для первой формы потери устойчивости. Для нее была справедлива и постановка Хоффа. Одной из задач исследования являлось в том числе исследование поведения стержня при формах потери устойчивости выше первой.

В постановке Хоффа не удалось получить даже вторую форму потери устойчивости. Как было доказано ранее на высоких скоростях результат КЭ моделирование не соответствует заявленной формуле, а на маленьких скоростях время расчета оказывалось настолько большим, что в системе появлялись ошибки еще до получения второй формы потери устойчивости.

Было решено поступить по аналогии с моделью Хоффа и задать изначальное несовершенство модели в двух местах таким образом, чтобы изначальная конфигурация соответствовала второй форме. Было проведено моделирование аналогичное прошлой части задачи.

Анализируя полученные результаты, можно утверждать, что полученная формула справедлива не только для первой формы потери устойчивости и позволяет исследовать и устойчивость более высоких порядков. Однако, сходимость КЭ моделирования второй формы потери устойчивости к аналитическому результату оказалась хуже, чем для первой. Это может быть связано как с недостаточной точностью моделирования, так и с влиянием более сложного несовершенства стержня. Стоит также подчеркнуть, что исследование второй формы в большей степени ограничивает применимость формулы. О достаточной точности можно говорить только при маленьких скоростях сжатия стержня. Нижний порог амплитуды несовершенства тоже оказался выше, чем для первой формы потери устойчивости, и имел порядок 10-4.

При переходе к тонкостенному стержню стоило ожидать отклонения от формулы из-за эффекта депланации, достигаемого раньше, чем общая потеря устойчивости. Однако моделирование показало возможность применения данной теории и для тонкостенных стержней.

Стоит отметить и определенные различия в результатах между тонкостенным и сплошным стержнями:

• моделирование тонкостенного стержня показало меньшую точность, чем моделирование сплошного профиля
• график зависимости силы от времени для всех комбинаций скорость-несовершенство имел существенные различия между тонкостенной и сплошной моделью, что, однако не помешало получению достаточно точного результата

Выводы

По результатам работы сделаны следующие выводы.

Использование оболочечного построения в ABAQUS упрощает модель без потери качества, поэтому для исследования статической формы потери была использована именно данная модель. При переходе к динамической форме устойчивости была использована балочная постановка.

Был скорректирован коэффициент запаса для учета податливости саморезов.

КЭ моделирование позволило подтвердить возможность использования формулы, полученной в статье [27], хотя и ограничило область ее применения. Были получены максимальные и минимальные условия для ее использования.

Было доказано, что исследование второй формы потери устойчивости не выходит за рамки используемой теории и позволяет получить достаточно точные результаты. Есть все основания полагать, что аналогичная картина будет наблюдаться и для более высоких форм потери устойчивости. Однако область применения формулы была ограничена сильнее, чем в случае первой формы.

Несмотря на локальную потерю устойчивости, результаты, полученные после исследования тонкостенного стержня, также согласуются с аналитикой, что открывает возможность для динамического тестирования тонкостенных профилей на разные случаи нагружения с последующим сравнением с формулой.

Список литературы

• Власов В. 3., Тонкостенные упругие стержни, 2 изд., М., 1959. О. В. Лужин.
• Georgieva IB, Schuereman L, Pyl L, Composed columns from cold-formed steel Z-profiles: Experiments and code-based predictions of the overall compression capacity. Engineering Structures 37 (2012)
• Abaqus/CAE User's Manual, Dassault Systèmes, 2012
• Hoff,N.J.: The dynamics of the buckling of elastic columns. J. Appl. Mech. 18, 68–74 (1951)
• Vitaly A. Kuzkin, Mona M. Dannert Buckling of a column under a constant speed compression: a dynamic correction to the Euler formula