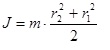Установка по определению момента инерции — различия между версиями
м |
м |
||
| (не показана 21 промежуточная версия этого же участника) | |||
| Строка 34: | Строка 34: | ||
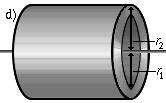
При расчетах момента инерции полого толстостенного цилиндра используется формула | При расчетах момента инерции полого толстостенного цилиндра используется формула | ||
| − | [[File:Формула_1.jpg|left| | + | [[File:Формула_1.jpg|left|]] |
| − | + | <br> | |
| − | + | <br> | |
| − | + | <br> | |
| − | где | + | где J-момент инерции полого толстостенного цилиндра, |
| − | |||
r<sub>1</sub> - внешний радиус цилиндра, | r<sub>1</sub> - внешний радиус цилиндра, | ||
r<sub>2</sub> - внутренний радиус цилиндра, | r<sub>2</sub> - внутренний радиус цилиндра, | ||
| − | m - масса цилиндра | + | m - масса цилиндра. |
| − | [[File:Цилиндр_1.png|left| | + | [[File:Цилиндр_1.png|left|]] |
| − | + | <br> | |
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
Найдём момент инерции, зная геометрические параметры тела и его массу. Для исследования был взят цилиндр с массой 1,8 кг, внешним радиусом 0,0575 м, внутренним радиусом 0,015 м. Используя приведенную формулу (1), получаем момент инерции: | Найдём момент инерции, зная геометрические параметры тела и его массу. Для исследования был взят цилиндр с массой 1,8 кг, внешним радиусом 0,0575 м, внутренним радиусом 0,015 м. Используя приведенную формулу (1), получаем момент инерции: | ||
| − | [[File:Формула_2.jpg|left| | + | [[File:Формула_2.jpg|left|]] |
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
Теперь рассмотрим динамический способ определения момента инерции. | Теперь рассмотрим динамический способ определения момента инерции. | ||
| − | В процессе вращательного движения на тело действует сила трения. Для расчета момента силы трения воспользуемся формулой File:Формула_3.jpg | + | В процессе вращательного движения на тело действует сила трения. Для расчета момента силы трения воспользуемся формулой: |
| + | |||
| + | [[File:Формула_3.jpg|left|]] | ||
| + | <br> | ||
| + | <br> | ||
| + | где M – момент силы трения, F – сила тяжести, r – радиус вала, вокруг которого вращается тело. | ||
| + | Известна также формула для расчета момента силы трения через угловое ускорение и момент инерции: | ||
| + | [[File:Формула_4.jpg|left|]] | ||
| + | <br> | ||
| + | <br> | ||
| + | где M – момент силы трения, J-момент инерции полого толстостенного цилиндра, ɛ- угловое ускорение. | ||
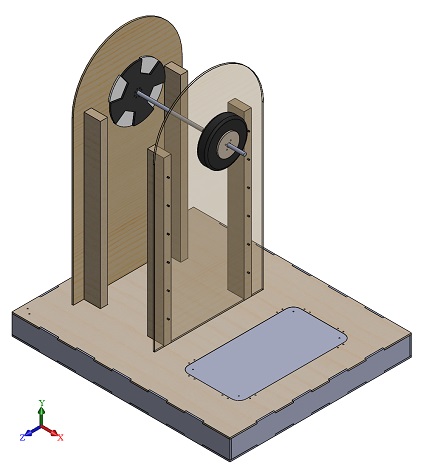
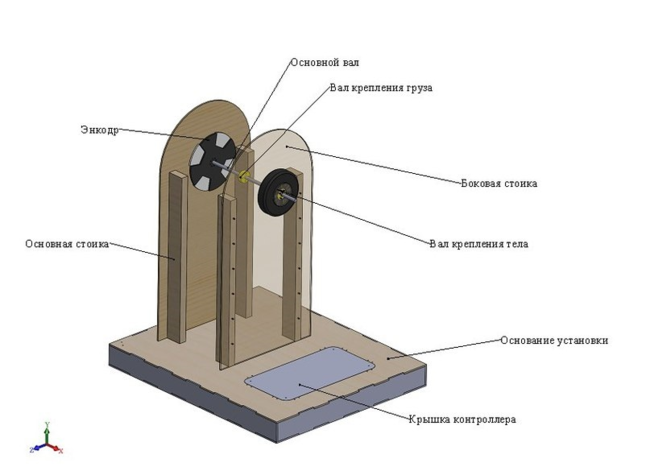
| + | Рассмотрим сконструированную в ходе работы установку, позволяющую получить значение углового ускорения при вращении толстостенного полого цилиндра . | ||
| + | |||
| + | [[File:Ustanovka2111.png|650px|left|]] | ||
| + | <br> | ||
| + | <br> | ||
| + | Грузу на вале сообщается угловая скорость, достаточная, чтобы нить с грузом известной массы полностью намоталась на вал. После чего вал с закреплённым на неё телом начинает раскручиваться грузом, опускающимся вниз. Для получения данных, используемых для нахождения углового ускорения, на внешнюю часть одной из боковых стенок установки под лопастную деталь был помещен датчик, фиксирующий промежутки времени, за которое каждая лопасть проходит мимо датчика. | ||
| + | [[File:Formula5.png|left|]] | ||
| + | [[File:Formula6.png|left|]] | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| − | [[File: | + | ===Описание эксперимента по расчету момента инерции полого толстостенного цилиндра=== |
| + | Для организации эксперимента была сконструирована установка, описанная выше. | ||
| + | На первом этапе в программе SolidWorks были созданы чертежи и 3D-модель установки. | ||
| + | [[File:Solid_ustanovki.jpg|500px|left|]] | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | На следующем этапе чертежи были переведены в формат DXF, позволяющий распечатку деталей на лазерном станке StepDir 150250 и 3D-принтере MakerBot. | ||
| + | Установка была собрана вручную. | ||
| + | Третий этап заключался в установке датчика и программировании контроллера Аrduino Uno. Для работы использовался датчик, реагирующий на изменения яркости света. Датчик был подключен к контроллеру, программа для которого была написана на языке программирования С++. | ||
| + | [[File:Прога.jpg|left|]] | ||
Текущая версия на 21:44, 17 июня 2016
Кафедра ТМ > Занятия со школьниками. Семинары, интенcивы, проекты
Куратор проекта:
- Опочанский А.А.
Участники:
- Давидович Борис 10 класс.
Содержание
Введение[править]
Любой закон физики рождается после теоретического осмысления большого числа закономерностей, полученных опытным путем. Таким образом, в основе изучения любого физического явления лежит эксперимент. Вращательное движение твердого тела вокруг неподвижной оси – это один из частных случаев механического движения. Как любое движение оно описывается различными характеристиками. Эти характеристики принято классифицировать на кинематические и динамические. К кинематическим характеристикам относятся такие понятия, как угловая скорость и угловое ускорение, линейная скорость, частота и период вращения. Динамической характеристикой вращательного движения является момент инерции. Способность тела препятствовать изменению своей скорости называется инертностью. Момент инерции – это физическая величина, являющаяся мерой инертности тела при вращательном движении. Фактически момент инерции показывает, какое усилие необходимо приложить к телу, совершающему вращательное движение, чтобы изменить его скорость. Одним из известных исследователей механического, в том числе вращательного, движения являлся голландский механик, астроном и математик Христиан Гюйгенс (1629-1695 гг.). Именно ему приписывают введение в науку самого понятия момента инерции [1; 8]. Другим ученым, внесшим значительный вклад в изучение вопроса о моменте инерции, является французский ученый Н. Перси (1834 г.). В предлагаемой работе рассматриваются как теоретические, так и практические методы определения момента инерции при различных видах вращательного движения.
Цель проекта[править]
Целью работы являются разработка, изготовление и апробация установки, позволяющей рассчитать момент инерции полого толстостенного цилиндра при вращательном движении, а также исследование вопроса о соответствии практического результата данным, полученным аналитически.
Объектом исследования[править]
Объектом исследования является полый толстостенный цилиндр.
Предмет исследования[править]
Предметом исследования является практический метод, позволяющий рассчитать момент инерции полого толстостенного цилиндра, с помощью сконструированной установки для измерения и расчета момента инерции. Для подготовки 3D – модели и чертежей установки была изучена и использована программа Solidworks. Детали установки изготовлены на лазерном станке StepDir 150250 и 3D-принтере MakerBot. Для считывания полученных данных в установке использовался контроллер Arduino Uno, запрограммированный на языке программирования C++.
Теоретические основы расчета момента инерции полого толстостенного цилиндра[править]
Задача расчета момента инерции полого толстостенного цилиндра решается при разработке многих инженерных проектов. При расчетах момента инерции полого толстостенного цилиндра используется формула
где J-момент инерции полого толстостенного цилиндра, r1 - внешний радиус цилиндра, r2 - внутренний радиус цилиндра, m - масса цилиндра.
Найдём момент инерции, зная геометрические параметры тела и его массу. Для исследования был взят цилиндр с массой 1,8 кг, внешним радиусом 0,0575 м, внутренним радиусом 0,015 м. Используя приведенную формулу (1), получаем момент инерции:
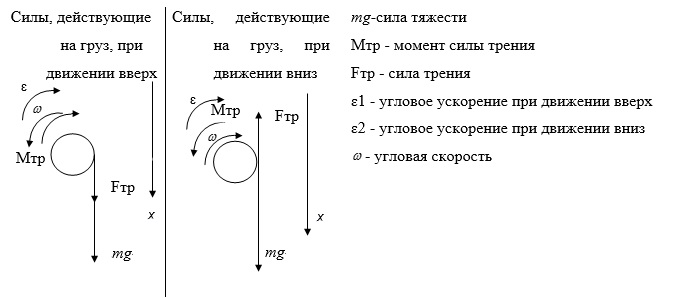
Теперь рассмотрим динамический способ определения момента инерции. В процессе вращательного движения на тело действует сила трения. Для расчета момента силы трения воспользуемся формулой:
где M – момент силы трения, F – сила тяжести, r – радиус вала, вокруг которого вращается тело.
Известна также формула для расчета момента силы трения через угловое ускорение и момент инерции:
где M – момент силы трения, J-момент инерции полого толстостенного цилиндра, ɛ- угловое ускорение.
Рассмотрим сконструированную в ходе работы установку, позволяющую получить значение углового ускорения при вращении толстостенного полого цилиндра .
Грузу на вале сообщается угловая скорость, достаточная, чтобы нить с грузом известной массы полностью намоталась на вал. После чего вал с закреплённым на неё телом начинает раскручиваться грузом, опускающимся вниз. Для получения данных, используемых для нахождения углового ускорения, на внешнюю часть одной из боковых стенок установки под лопастную деталь был помещен датчик, фиксирующий промежутки времени, за которое каждая лопасть проходит мимо датчика.
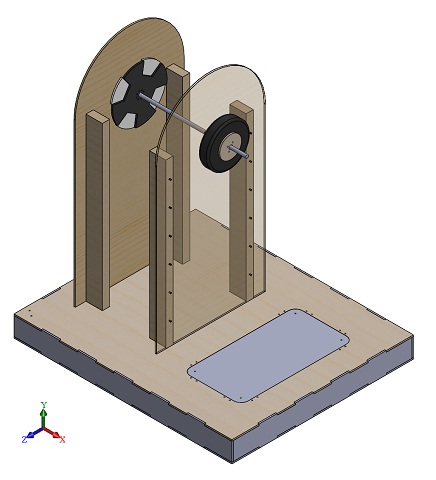
Описание эксперимента по расчету момента инерции полого толстостенного цилиндра[править]
Для организации эксперимента была сконструирована установка, описанная выше. На первом этапе в программе SolidWorks были созданы чертежи и 3D-модель установки.
На следующем этапе чертежи были переведены в формат DXF, позволяющий распечатку деталей на лазерном станке StepDir 150250 и 3D-принтере MakerBot.
Установка была собрана вручную.
Третий этап заключался в установке датчика и программировании контроллера Аrduino Uno. Для работы использовался датчик, реагирующий на изменения яркости света. Датчик был подключен к контроллеру, программа для которого была написана на языке программирования С++.