Cilinder — различия между версиями
Savoliiy (обсуждение | вклад) |
Savoliiy (обсуждение | вклад) |
||
| Строка 11: | Строка 11: | ||
| − | * Второй закон Ньютона: Ускорение, приобретаемое телом в результате воздействия на него, прямо пропорционально силе или равнодействующей сил этого воздействия и обратно пропорционально массе тела | + | * Второй закон Ньютона: Ускорение, приобретаемое телом в результате воздействия на него, прямо пропорционально силе или равнодействующей сил этого воздействия и обратно пропорционально массе тела: F=ma |
| − | *Момент инерции: Скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). | + | *Момент инерции: Скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Момент инерции цилиндра: J=J<sub>0</sub>+mR<sup>2</sup> |
| − | Момент инерции цилиндра: J=J<sub>0</sub>+mR<sup>2</sup> | ||
| − | * Угловая скорость: физическая величина, равная отношению угла поворота к интервалу времени, в течение которого этот поворот произошел. | + | * Угловая скорость: физическая величина, равная отношению угла поворота к интервалу времени, в течение которого этот поворот произошел. Связь угловой и линейной скоростей: υ=ωR |
| − | Связь угловой и линейной скоростей: υ=ωR | ||
| − | * Сила трения качения: Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого | + | * Сила трения качения: Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого: F<sub>качения</sub>=f*N/R |
| − | F<sub>качения</sub>=f*N/R | + | |
== Результаты работы программы == | == Результаты работы программы == | ||
Версия 16:33, 17 июня 2016
- Исполнитель:Савельева Ольга
- Группа:13604/1
- Семестр:Весна 2016
Содержание
Аннотация
Данная курсовая работа рассматривает движение полого деревянного цилиндра. Полый цилиндр скатывается с плоскости, находящейся под некоторым углом, на горизонтальную плоскость. Спустя какое-то время он останавливается. Данная программа вычисляет время с момента начала скатывания с плоскости, находящейся под углом, до его полной остановки.
Основные определения и понятия
- Второй закон Ньютона: Ускорение, приобретаемое телом в результате воздействия на него, прямо пропорционально силе или равнодействующей сил этого воздействия и обратно пропорционально массе тела: F=ma
- Момент инерции: Скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Момент инерции цилиндра: J=J0+mR2
- Угловая скорость: физическая величина, равная отношению угла поворота к интервалу времени, в течение которого этот поворот произошел. Связь угловой и линейной скоростей: υ=ωR
- Сила трения качения: Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого: Fкачения=f*N/R
Результаты работы программы
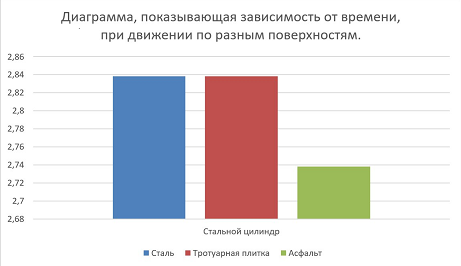
Программа вычисляет время падения цилиндра от начала скатывания до его полной остановки.
Мы рассмотрели 3 различных материала, по которым движется цилиндр и заметили, что время до полной остановки меняется незначительно, что можно увидеть на диаграмме:
Список литературы
Роберт Лафоре “Объектно-ориентированное программирование в C++”, 4-е издание (2004)
http://physics.nad.ru/Physics/Cyrillic/angl_txt.htm
Ф. Л. Черноусько, Л. Д. Акуленко, Д. Д. Лещенко “Эволюция движения тела относительно центра масс” (2015)
Курсовую работы вы можете скачать