Свободные колебания платформы в вертикальной плоскости — различия между версиями
| (не показано 5 промежуточных версий 3 участников) | |||
| Строка 2: | Строка 2: | ||
'''Что собой представляет система '''<br /> | '''Что собой представляет система '''<br /> | ||
| − | Платформа, закрепленная на пружинах, совершает колебания в вертикальной плоскости. | + | Платформа, закрепленная на пружинах, совершает колебания в вертикальной плоскости (задача с одной степенью свободы). |
'''Постановка задачи'''<br /> | '''Постановка задачи'''<br /> | ||
| − | Исследовать свободные колебания платформы массы <math>{M}</math>, если расстояние центра тяжести платформы от вертикальных плоскостей, проведенных через оси колесных пар, <math>l_{1} = l_{2} = l</math>. Радиус инерции относительно центральной поперечной оси вагона <math>i_{Cy}</math>, жесткость рессор для всех осей одинакова и равна <math> | + | Исследовать свободные колебания платформы массы <math>{M}</math>, если расстояние центра тяжести платформы от вертикальных плоскостей, проведенных через оси колесных пар, <math>l_{1} = l_{2} = l</math>. Радиус инерции относительно центральной поперечной оси вагона <math>i_{Cy}</math>, жесткость рессор для всех осей одинакова и равна <math>c |
| + | </math>. Массой рессор и силами трения пренебрегаем. | ||
| − | [[Файл: | + | [[Файл: platform_1.jpg|500px|]] |
'''Основные уравнения'''<br /> | '''Основные уравнения'''<br /> | ||
<math> | <math> | ||
| − | + | T=\frac{1}{2}\frac{G}{g}i_{Cy}^{2}\dot{\phi}^{2}\\ | |
| − | + | P=\frac{1}{2}4cl^{2}\phi^{2}\\ | |
| + | \ddot{\phi}+\frac{4cl^{2}g}{Gi_{Cy}^{2}}\phi=0\\ | ||
| + | a_{1}=\frac{G}{g}i_{Cy}^{2}\\ | ||
| + | c_{1}=4cl^{2}\\ | ||
</math> | </math> | ||
| − | + | Частота главных колебаний | |
<math> | <math> | ||
| − | k_{1}=\sqrt{\frac{c_{1}}{a_{1 | + | k_{1}=\sqrt{\frac{c_{1}}{a_{1}}}=\sqrt{\frac{4cl^{2}g}{Gi_{Cy}^{2}}} |
| − | |||
</math> | </math> | ||
| − | + | Уравнение движения системы | |
<math> | <math> | ||
| − | + | \phi=C_{1}sin(k_{1}t+\alpha_{1}) | |
| − | |||
</math> | </math> | ||
| + | |||
| + | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Fedorenko/spring/maxf_1.html |width=1000 |height=800 |border=0 }} | ||
| + | |||
| + | Скачать [[Медиа:platform.rar|platform.rar]]. | ||
| + | |||
| + | <div class="mw-collapsible mw-collapsed" style="width:100%" > | ||
| + | '''Текст программы на языке JavaScript (разработчик [[Федоренко Максим]]):''' <div class="mw-collapsible-content"> | ||
| + | Файл '''"Spring.js"''' | ||
| + | <syntaxhighlight lang="javascript" line start="1" enclose="div"> | ||
| + | window.addEventListener("load", Main_Spring, true); | ||
| + | function Main_Spring() { | ||
| + | |||
| + | var canvas = spring_canvas; | ||
| + | canvas.onselectstart = function () {return false;}; // запрет выделения canvas | ||
| + | var ctx = canvas.getContext("2d"); // на ctx происходит рисование | ||
| + | var w = canvas.width; // ширина окна в расчетных координатах | ||
| + | var h = canvas.height; // высота окна в расчетных координатах | ||
| + | |||
| + | var Pi = Math.PI; // число "пи" | ||
| + | var g = 9.81; | ||
| + | var m0 = 1; // масштаб массы | ||
| + | var T0 = 1; // масштаб времени (период колебаний исходной системы) | ||
| + | var dz = 0; | ||
| + | var k0 = 2 * Pi / T0; // масштаб частоты | ||
| + | var C0 = 1; // масштаб жесткости | ||
| + | var D0 = 0.001; // диаметра | ||
| + | var p0 = 1; // давление | ||
| + | var E0 = 1; | ||
| + | var L = 300; | ||
| + | // *** Задание физических параметров *** | ||
| + | var E = 2.05e5 * E0; // модуль упругости | ||
| + | var m = 3 * m0; // масса | ||
| + | var C = 15 * C0; // жесткость | ||
| + | var phi0 = 0; | ||
| + | slider_m.value = (m / m0).toFixed(1); number_m.value = (m / m0).toFixed(1); | ||
| + | slider_C.value = (C / C0).toFixed(1); number_C.value = (C / C0).toFixed(1); | ||
| + | slider_phi.value = (phi0).toFixed(1); number_phi.value = (phi0).toFixed(1); | ||
| + | |||
| + | // *** Задание вычислительных параметров *** | ||
| + | |||
| + | var fps = 100; // frames per second - число кадров в секунду (качечтво отображения) | ||
| + | var spf = 50; // steps per frame - число шагов интегрирования между кадрами (edtkbxbdftn скорость расчета) | ||
| + | var dt = 0.05 * T0 / fps; // шаг интегрирования (качество расчета) | ||
| + | var steps = 0; // количество шагов интегрирования | ||
| + | var dx = 150; | ||
| + | function setM(new_m) {m = new_m * m0;} | ||
| + | function setC(new_C) {C = new_C * C0;} | ||
| + | function setphi(new_phi) {phi0 = new_phi; dz = 30*Math.sin(phi0*Math.PI/180); rect.y=rect.y+dz; console.log(phi0);} | ||
| + | |||
| + | slider_m.oninput = function() {number_m.value = slider_m.value; setM(slider_m.value);}; | ||
| + | number_m.oninput = function() {slider_m.value = number_m.value; setM(number_m.value);}; | ||
| + | slider_C.oninput = function() {number_C.value = slider_C.value; setC(slider_C.value);}; | ||
| + | number_C.oninput = function() {slider_C.value = number_C.value; setC(number_C.value);}; | ||
| + | slider_phi.oninput = function() {number_phi.value = slider_phi.value; setphi(slider_phi.value);}; | ||
| + | number_phi.oninput = function() {slider_phi.value = number_phi.value; setphi(number_phi.value);}; | ||
| + | |||
| + | var count = true; // проводить ли расчет системы | ||
| + | var v = 0; // скорость тела | ||
| + | |||
| + | var rw = canvas.width / 10; var rh = canvas.height; | ||
| + | var x0 = canvas.width / 2; var y0 = rh/2; | ||
| + | |||
| + | // параметры пружины | ||
| + | var coil = 11; // количество витков | ||
| + | var startY = h; // закрепление пружины | ||
| + | |||
| + | // создаем прямоугольник-грузик | ||
| + | var rect = { | ||
| + | x: x0, width: dx, | ||
| + | y: y0, height: 20, | ||
| + | fill: "rgba(112, 155, 255, 1)" // цвет | ||
| + | }; | ||
| + | |||
| + | // график | ||
| + | var vGraph = new New_graph( // определить график | ||
| + | "#vGraph", // на html-элементе #vGraph | ||
| + | 250, // сколько шагов по оси "x" отображается | ||
| + | -1, 1, 0.2); // мин. значение оси Y, макс. значение оси Y, шаг по оси Y | ||
| + | |||
| + | function control() { | ||
| + | calculate(); | ||
| + | draw(); | ||
| + | requestAnimationFrame(control); | ||
| + | } | ||
| + | control(); | ||
| + | // setInterval(control, 1000 / fps); // Запуск системы | ||
| + | |||
| + | |||
| + | function calculate() { | ||
| + | if (!count) return; | ||
| + | for (var s=1; s<=spf; s++) { | ||
| + | var f = - C * (rect.y - y0); | ||
| + | v += f / m * dt; | ||
| + | rect.y += v * dt; | ||
| + | steps++; | ||
| + | if (steps % 80 == 0) vGraph.graphIter(steps, -(rect.y-y0)/canvas.height*2); // подать данные на график | ||
| + | } | ||
| + | |||
| + | } | ||
| + | function draw() { | ||
| + | ctx.clearRect(0, 0, w, h); | ||
| + | ctx.fillStyle = "#4B4747"; | ||
| + | ctx.beginPath(); | ||
| + | ctx.moveTo(rect.x-dx,rect.y); | ||
| + | ctx.lineTo(rect.x+dx,2*y0-rect.y); | ||
| + | ctx.lineWidth = 20; | ||
| + | ctx.stroke(); | ||
| + | ctx.lineWidth = 1; | ||
| + | draw_spring(rect.x-dx, rect.x-dx, rh-50, rect.y+dz/2, 20, 10); | ||
| + | draw_spring(rect.x+dx, rect.x+dx, rh-50, 2*y0-rect.y-dz/2, 20, 10); | ||
| + | ctx.fillStyle = "#4B4747"; | ||
| + | ctx.beginPath(); | ||
| + | ctx.arc(rect.x-dx, rh-50, 50 , 0, Math.PI*2, true); | ||
| + | ctx.arc(rect.x+dx, rh-50, 50 , 0, Math.PI*2, true); | ||
| + | ctx.closePath(); | ||
| + | ctx.fill(); | ||
| + | |||
| + | } | ||
| + | |||
| + | function draw_spring(x_start, x_end, y_start, y_end, h, n) { | ||
| + | var L_x = x_end-x_start; | ||
| + | var L_y = y_end-y_start; | ||
| + | for (var i = 0; i < n; i++) { | ||
| + | var x_st = x_start + L_x / n * i; | ||
| + | var x_end = x_start + L_x / n * (i + 1); | ||
| + | var y_st = y_start + L_y / n * i; | ||
| + | var y_end = y_start + L_y / n * (i + 1); | ||
| + | var l_x = x_end - x_st; | ||
| + | var l_y = y_end - y_st; | ||
| + | ctx.beginPath(); | ||
| + | ctx.bezierCurveTo(x_st , y_st , (x_st + l_x / 4 + h) , (y_st + l_y / 4) , (x_st + l_x / 2) , (y_st + l_y /2)); | ||
| + | ctx.bezierCurveTo((x_st + l_x / 2) , (y_st + l_y / 2) , (x_st + 3 * l_x / 4 - h) , (y_st + 3 * l_y / 4) , (x_st + l_x) , (y_st + l_y)) ; | ||
| + | ctx.stroke(); | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | function New_graph(htmlElement, yArrayLen, minY, maxY, stepY){ | ||
| + | this.htmlElement = htmlElement; | ||
| + | this.yArrayLen = yArrayLen; | ||
| + | this.minY = minY; | ||
| + | this.maxY = maxY; | ||
| + | this.stepY = stepY; | ||
| + | this.vArray = []; | ||
| + | } | ||
| + | New_graph.prototype.graphIter = function(x, y){ | ||
| + | this.vArray.push([x, y]); // добавляем значение в конец массива | ||
| + | if (this.vArray.length > this.yArrayLen) this.vArray.shift(); // если в массиве больше yArrayLen значений - удаляем первое | ||
| + | var htmlElement1 = this.htmlElement; | ||
| + | var vArray1 = this.vArray; | ||
| + | var minY1 = this.minY; | ||
| + | var maxY1 = this.maxY; | ||
| + | var stepY1 = this.stepY; | ||
| + | $(function() { | ||
| + | var options = { | ||
| + | yaxis: { | ||
| + | min: minY1, | ||
| + | max: maxY1, | ||
| + | tickSize: stepY1 | ||
| + | } | ||
| + | }; | ||
| + | $.plot(htmlElement1, [vArray1], options); // рисуем график на элементе "vGraph" | ||
| + | }); | ||
| + | }; | ||
| + | |||
| + | New_graph.prototype.graph = function(data){ | ||
| + | this.vArray = data; | ||
| + | var htmlElement1 = this.htmlElement; | ||
| + | var vArray1 = this.vArray; | ||
| + | var minY1 = this.minY; | ||
| + | var maxY1 = this.maxY; | ||
| + | var stepY1 = this.stepY; | ||
| + | $(function() { | ||
| + | var options = { | ||
| + | yaxis: { | ||
| + | min: minY1, | ||
| + | max: maxY1, | ||
| + | tickSize: stepY1 | ||
| + | } | ||
| + | }; | ||
| + | $.plot(htmlElement1, [vArray1], options); // рисуем график на элементе "vGraph" | ||
| + | }); | ||
| + | }; | ||
| + | |||
| + | |||
| + | |||
| + | function New(){} | ||
| + | New.prototype.addSlider = function(htmlSliderElement, htmlValueElement, minVal, maxVal, stepVal, startVal, setFunc){ | ||
| + | $(function() { | ||
| + | $( htmlSliderElement ).slider({ // слайдер на div - элемент "slider_m" | ||
| + | value:startVal, min: minVal, max: maxVal, step: stepVal, | ||
| + | slide: function( event, ui ) { // работает во время движения слайдера | ||
| + | $( htmlValueElement ).text( ui.value.toFixed(2) ); // присваивает значение текстовому полю "value_m" | ||
| + | setFunc(ui.value); | ||
| + | } | ||
| + | }); | ||
| + | }); | ||
| + | }; | ||
| + | New.prototype.addInputSlider = function(htmlSliderElement, htmlValueElement, minVal, maxVal, stepVal, startVal, setFunc, pressFunc){ | ||
| + | window[pressFunc] = function(event){ | ||
| + | var regExpPattern = /[0-9]+[.]?[0-9]+/; | ||
| + | var inputVal = document.getElementById(htmlValueElement.substr(1)).value; | ||
| + | if (regExpPattern.test(inputVal.toString()) && inputVal != 0){setFunc(inputVal);} | ||
| + | }; | ||
| + | |||
| + | $(function() { | ||
| + | $( htmlSliderElement ).slider({ | ||
| + | value:startVal, min: minVal, max: maxVal, step: stepVal, | ||
| + | slide: function( event, ui ) { | ||
| + | $( htmlValueElement ).val( ui.value.toFixed(2) ); | ||
| + | setFunc(ui.value); | ||
| + | } | ||
| + | }); | ||
| + | $( htmlValueElement ).val($( htmlSliderElement ).slider( "value" ).toFixed(2) ); | ||
| + | }); | ||
| + | }; | ||
Текущая версия на 12:07, 13 апреля 2016
Виртуальная лаборатория>Свободные колебания платформы в вертикальной плоскостиЧто собой представляет система
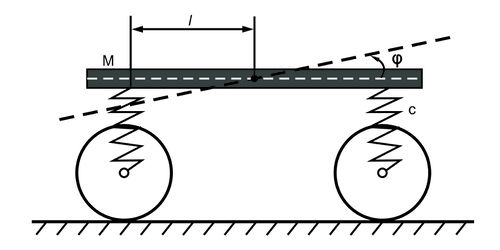
Платформа, закрепленная на пружинах, совершает колебания в вертикальной плоскости (задача с одной степенью свободы).
Постановка задачи
Исследовать свободные колебания платформы массы , если расстояние центра тяжести платформы от вертикальных плоскостей, проведенных через оси колесных пар, . Радиус инерции относительно центральной поперечной оси вагона , жесткость рессор для всех осей одинакова и равна . Массой рессор и силами трения пренебрегаем.
Основные уравнения
Частота главных колебаний
Уравнение движения системы
Скачать platform.rar.
Файл "Spring.js" <syntaxhighlight lang="javascript" line start="1" enclose="div"> window.addEventListener("load", Main_Spring, true); function Main_Spring() {
var canvas = spring_canvas;
canvas.onselectstart = function () {return false;}; // запрет выделения canvas
var ctx = canvas.getContext("2d"); // на ctx происходит рисование
var w = canvas.width; // ширина окна в расчетных координатах
var h = canvas.height; // высота окна в расчетных координатах
var Pi = Math.PI; // число "пи"
var g = 9.81;
var m0 = 1; // масштаб массы var T0 = 1; // масштаб времени (период колебаний исходной системы)
var dz = 0;
var k0 = 2 * Pi / T0; // масштаб частоты var C0 = 1; // масштаб жесткости var D0 = 0.001; // диаметра
var p0 = 1; // давление var E0 = 1; var L = 300;
// *** Задание физических параметров ***
var E = 2.05e5 * E0; // модуль упругости
var m = 3 * m0; // масса var C = 15 * C0; // жесткость var phi0 = 0;
slider_m.value = (m / m0).toFixed(1); number_m.value = (m / m0).toFixed(1);
slider_C.value = (C / C0).toFixed(1); number_C.value = (C / C0).toFixed(1); slider_phi.value = (phi0).toFixed(1); number_phi.value = (phi0).toFixed(1);
// *** Задание вычислительных параметров ***
var fps = 100; // frames per second - число кадров в секунду (качечтво отображения) var spf = 50; // steps per frame - число шагов интегрирования между кадрами (edtkbxbdftn скорость расчета) var dt = 0.05 * T0 / fps; // шаг интегрирования (качество расчета) var steps = 0; // количество шагов интегрирования
var dx = 150;
function setM(new_m) {m = new_m * m0;}
function setC(new_C) {C = new_C * C0;}
function setphi(new_phi) {phi0 = new_phi; dz = 30*Math.sin(phi0*Math.PI/180); rect.y=rect.y+dz; console.log(phi0);}
slider_m.oninput = function() {number_m.value = slider_m.value; setM(slider_m.value);};
number_m.oninput = function() {slider_m.value = number_m.value; setM(number_m.value);};
slider_C.oninput = function() {number_C.value = slider_C.value; setC(slider_C.value);};
number_C.oninput = function() {slider_C.value = number_C.value; setC(number_C.value);};
slider_phi.oninput = function() {number_phi.value = slider_phi.value; setphi(slider_phi.value);};
number_phi.oninput = function() {slider_phi.value = number_phi.value; setphi(number_phi.value);};
var count = true; // проводить ли расчет системы var v = 0; // скорость тела
var rw = canvas.width / 10; var rh = canvas.height; var x0 = canvas.width / 2; var y0 = rh/2;
// параметры пружины var coil = 11; // количество витков var startY = h; // закрепление пружины
// создаем прямоугольник-грузик
var rect = {
x: x0, width: dx,
y: y0, height: 20,
fill: "rgba(112, 155, 255, 1)" // цвет
};
// график
var vGraph = new New_graph( // определить график
"#vGraph", // на html-элементе #vGraph
250, // сколько шагов по оси "x" отображается
-1, 1, 0.2); // мин. значение оси Y, макс. значение оси Y, шаг по оси Y
function control() {
calculate();
draw();
requestAnimationFrame(control);
}
control();
// setInterval(control, 1000 / fps); // Запуск системы
function calculate() {
if (!count) return;
for (var s=1; s<=spf; s++) {
var f = - C * (rect.y - y0);
v += f / m * dt;
rect.y += v * dt;
steps++;
if (steps % 80 == 0) vGraph.graphIter(steps, -(rect.y-y0)/canvas.height*2); // подать данные на график
}
}
function draw() {
ctx.clearRect(0, 0, w, h);
ctx.fillStyle = "#4B4747"; ctx.beginPath(); ctx.moveTo(rect.x-dx,rect.y); ctx.lineTo(rect.x+dx,2*y0-rect.y); ctx.lineWidth = 20; ctx.stroke(); ctx.lineWidth = 1; draw_spring(rect.x-dx, rect.x-dx, rh-50, rect.y+dz/2, 20, 10); draw_spring(rect.x+dx, rect.x+dx, rh-50, 2*y0-rect.y-dz/2, 20, 10); ctx.fillStyle = "#4B4747"; ctx.beginPath(); ctx.arc(rect.x-dx, rh-50, 50 , 0, Math.PI*2, true); ctx.arc(rect.x+dx, rh-50, 50 , 0, Math.PI*2, true);
ctx.closePath(); ctx.fill();
}
function draw_spring(x_start, x_end, y_start, y_end, h, n) { var L_x = x_end-x_start;
var L_y = y_end-y_start;
for (var i = 0; i < n; i++) {
var x_st = x_start + L_x / n * i;
var x_end = x_start + L_x / n * (i + 1);
var y_st = y_start + L_y / n * i;
var y_end = y_start + L_y / n * (i + 1);
var l_x = x_end - x_st;
var l_y = y_end - y_st;
ctx.beginPath();
ctx.bezierCurveTo(x_st , y_st , (x_st + l_x / 4 + h) , (y_st + l_y / 4) , (x_st + l_x / 2) , (y_st + l_y /2));
ctx.bezierCurveTo((x_st + l_x / 2) , (y_st + l_y / 2) , (x_st + 3 * l_x / 4 - h) , (y_st + 3 * l_y / 4) , (x_st + l_x) , (y_st + l_y)) ;
ctx.stroke();
}
}
} function New_graph(htmlElement, yArrayLen, minY, maxY, stepY){
this.htmlElement = htmlElement; this.yArrayLen = yArrayLen; this.minY = minY; this.maxY = maxY; this.stepY = stepY; this.vArray = [];
} New_graph.prototype.graphIter = function(x, y){
this.vArray.push([x, y]); // добавляем значение в конец массива
if (this.vArray.length > this.yArrayLen) this.vArray.shift(); // если в массиве больше yArrayLen значений - удаляем первое
var htmlElement1 = this.htmlElement;
var vArray1 = this.vArray;
var minY1 = this.minY;
var maxY1 = this.maxY;
var stepY1 = this.stepY;
$(function() {
var options = {
yaxis: {
min: minY1,
max: maxY1,
tickSize: stepY1
}
};
$.plot(htmlElement1, [vArray1], options); // рисуем график на элементе "vGraph"
});
};
New_graph.prototype.graph = function(data){
this.vArray = data;
var htmlElement1 = this.htmlElement;
var vArray1 = this.vArray;
var minY1 = this.minY;
var maxY1 = this.maxY;
var stepY1 = this.stepY;
$(function() {
var options = {
yaxis: {
min: minY1,
max: maxY1,
tickSize: stepY1
}
};
$.plot(htmlElement1, [vArray1], options); // рисуем график на элементе "vGraph"
});
};
function New(){} New.prototype.addSlider = function(htmlSliderElement, htmlValueElement, minVal, maxVal, stepVal, startVal, setFunc){
$(function() {
$( htmlSliderElement ).slider({ // слайдер на div - элемент "slider_m"
value:startVal, min: minVal, max: maxVal, step: stepVal,
slide: function( event, ui ) { // работает во время движения слайдера
$( htmlValueElement ).text( ui.value.toFixed(2) ); // присваивает значение текстовому полю "value_m"
setFunc(ui.value);
}
});
});
}; New.prototype.addInputSlider = function(htmlSliderElement, htmlValueElement, minVal, maxVal, stepVal, startVal, setFunc, pressFunc){
window[pressFunc] = function(event){
var regExpPattern = /[0-9]+[.]?[0-9]+/;
var inputVal = document.getElementById(htmlValueElement.substr(1)).value;
if (regExpPattern.test(inputVal.toString()) && inputVal != 0){setFunc(inputVal);}
};
$(function() {
$( htmlSliderElement ).slider({
value:startVal, min: minVal, max: maxVal, step: stepVal,
slide: function( event, ui ) {
$( htmlValueElement ).val( ui.value.toFixed(2) );
setFunc(ui.value);
}
});
$( htmlValueElement ).val($( htmlSliderElement ).slider( "value" ).toFixed(2) );
});
};