Расчет определённого интеграла. Фролова Ксения. 6 курс — различия между версиями
(→Результаты) |
(→Реализация) |
||
| (не показано 15 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
==Постановка задачи== | ==Постановка задачи== | ||
Необходимо вычислить определенный интеграл <math>\int^1_0x^2dx</math> с использованием средств параллельного программирования на основе MPI. | Необходимо вычислить определенный интеграл <math>\int^1_0x^2dx</math> с использованием средств параллельного программирования на основе MPI. | ||
| + | ==Используемый метод== | ||
| + | В вычислительных системах с распределенной памятью процессоры работают независимо друг от друга. Для организации параллельных вычислений в таких условиях необходимо иметь возможность распределять вычислительную нагрузку и организовать информационное взаимодействие (передачу данных) между процессорами. Параллельное программирование служит для создания программ, эффективно использующих вычислительные ресурсы за счет одновременного исполнения кода на нескольких вычислительных узлах. Для создания параллельных приложений используются параллельные языки программирования и специализированные системы поддержки параллельного программирования, такие как MPI и OpenMP. Итак, MPI - это библиотека передачи сообщений, собрание функций на C/C++ (или подпрограмм в Фортране), облегчающих коммуникацию (обмен данными и синхронизацию задач) между процессами параллельной программы с распределенной памятью. Акроним MPI установлен для Message Passing Interface (интерфейс передачи сообщений). Под параллельной программой в рамках MPI понимается множество одновременно выполняемых процессов. Все процессы порождаются один раз, образуя параллельную часть программы. Каждый процесс работает в своем адресном пространстве, никаких общих переменных или данных в MPI нет. Процессы могут выполняться на разных процессорах, но на одном процессоре могут располагаться и несколько процессов (в этом случае их исполнение осуществляется в режиме разделения времени). | ||
| + | |||
==Реализация== | ==Реализация== | ||
Для расчета указанного интеграла используется метод трапеций - метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подинтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. | Для расчета указанного интеграла используется метод трапеций - метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подинтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. | ||
Отрезок [a..b] (в данной задаче [0..1]) разбивается на заданное количество интервалов (в данной задаче n=100000000), и на каждом из элементарных отрезков применяется формула трапеций. Cуммирование даст составную формулу трапеций:<br> | Отрезок [a..b] (в данной задаче [0..1]) разбивается на заданное количество интервалов (в данной задаче n=100000000), и на каждом из элементарных отрезков применяется формула трапеций. Cуммирование даст составную формулу трапеций:<br> | ||
<math>\int^b_a f(x)\,dx \approx \sum_{i=0}^{n-1} \frac{ f(x_i) + f(x_{i+1}) }{2} (x_{i+1} - x_{i}) </math> | <math>\int^b_a f(x)\,dx \approx \sum_{i=0}^{n-1} \frac{ f(x_i) + f(x_{i+1}) }{2} (x_{i+1} - x_{i}) </math> | ||
| − | Заданное количество интервалов распределяется между определенным количеством процессов. На каждом полученном таким способом интервале процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы соседние процессы должны обмениваться крайними значениями, полученными на предыдущем шаге, для выполнения следующего шага. Так, каждый процесс рассчитывает определенное количество интервалов по методу трапеций и обменивается информацией с соседними процессами. Суммируя результаты, полученные каждым отдельным процессом, мы получаем конечный результат. | + | Заданное количество интервалов распределяется между определенным количеством процессов. На каждом полученном таким способом интервале процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы соседние процессы должны обмениваться крайними значениями, полученными на предыдущем шаге, для выполнения следующего шага. Так, каждый процесс рассчитывает определенное количество интервалов по методу трапеций и обменивается информацией с соседними процессами. Суммируя результаты, полученные каждым отдельным процессом, мы получаем конечный результат.<br> |
| − | Программа, выполняющая расчет интеграла: | + | Программа, выполняющая расчет интеграла:[[Медиа:Integral_Frolova.7z| программа]] |
==Результаты== | ==Результаты== | ||
Вычислен определенный интеграл <math>\int^1_0x^2dx</math>.<br> | Вычислен определенный интеграл <math>\int^1_0x^2dx</math>.<br> | ||
| − | Показано, что при увеличении количества процессов уменьшается время расчета. | + | {| class="wikitable" width="300" floating="center" |
| + | !Количество процессов [-] | ||
| + | !Время рассчета [сек] | ||
| + | |- | ||
| + | |1 | ||
| + | |0.612851 | ||
| + | |- | ||
| + | |3 | ||
| + | |0.217436 | ||
| + | |- | ||
| + | |5 | ||
| + | |0.138726 | ||
| + | |- | ||
| + | |7 | ||
| + | |0.115826 | ||
| + | |- | ||
| + | |15 | ||
| + | |0.089728 | ||
| + | |- | ||
| + | |35 | ||
| + | |0.089625 | ||
| + | |} | ||
| + | <gallery widths=356px heights=233px perrow = 1> | ||
| + | Файл:Plot_x_2.jpg | ||
| + | </gallery> | ||
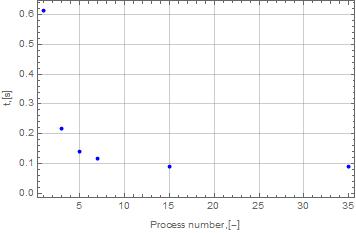
| + | Показано, что при увеличении количества процессов уменьшается время расчета. Также из приведенного графика видно, что для малого числа узлов в сетке использование большого количества процессов не обосновано - выигрыш во времени либо незначителен, либо же затраченное время увеличивается. | ||
Текущая версия на 14:47, 19 января 2016
Постановка задачи[править]
Необходимо вычислить определенный интеграл с использованием средств параллельного программирования на основе MPI.
Используемый метод[править]
В вычислительных системах с распределенной памятью процессоры работают независимо друг от друга. Для организации параллельных вычислений в таких условиях необходимо иметь возможность распределять вычислительную нагрузку и организовать информационное взаимодействие (передачу данных) между процессорами. Параллельное программирование служит для создания программ, эффективно использующих вычислительные ресурсы за счет одновременного исполнения кода на нескольких вычислительных узлах. Для создания параллельных приложений используются параллельные языки программирования и специализированные системы поддержки параллельного программирования, такие как MPI и OpenMP. Итак, MPI - это библиотека передачи сообщений, собрание функций на C/C++ (или подпрограмм в Фортране), облегчающих коммуникацию (обмен данными и синхронизацию задач) между процессами параллельной программы с распределенной памятью. Акроним MPI установлен для Message Passing Interface (интерфейс передачи сообщений). Под параллельной программой в рамках MPI понимается множество одновременно выполняемых процессов. Все процессы порождаются один раз, образуя параллельную часть программы. Каждый процесс работает в своем адресном пространстве, никаких общих переменных или данных в MPI нет. Процессы могут выполняться на разных процессорах, но на одном процессоре могут располагаться и несколько процессов (в этом случае их исполнение осуществляется в режиме разделения времени).
Реализация[править]
Для расчета указанного интеграла используется метод трапеций - метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подинтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями.
Отрезок [a..b] (в данной задаче [0..1]) разбивается на заданное количество интервалов (в данной задаче n=100000000), и на каждом из элементарных отрезков применяется формула трапеций. Cуммирование даст составную формулу трапеций:
Заданное количество интервалов распределяется между определенным количеством процессов. На каждом полученном таким способом интервале процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы соседние процессы должны обмениваться крайними значениями, полученными на предыдущем шаге, для выполнения следующего шага. Так, каждый процесс рассчитывает определенное количество интервалов по методу трапеций и обменивается информацией с соседними процессами. Суммируя результаты, полученные каждым отдельным процессом, мы получаем конечный результат.
Программа, выполняющая расчет интеграла: программа
Результаты[править]
Вычислен определенный интеграл .
| Количество процессов [-] | Время рассчета [сек] |
|---|---|
| 1 | 0.612851 |
| 3 | 0.217436 |
| 5 | 0.138726 |
| 7 | 0.115826 |
| 15 | 0.089728 |
| 35 | 0.089625 |
Показано, что при увеличении количества процессов уменьшается время расчета. Также из приведенного графика видно, что для малого числа узлов в сетке использование большого количества процессов не обосновано - выигрыш во времени либо незначителен, либо же затраченное время увеличивается.