Расчет определённого интеграла. Фролова Ксения. 6 курс — различия между версиями
(→Результаты) |
(→Результаты) |
||
| Строка 11: | Строка 11: | ||
Вычислен определенный интеграл <math>\int^1_0x^2dx</math>.<br> | Вычислен определенный интеграл <math>\int^1_0x^2dx</math>.<br> | ||
Показано, что при увеличении количества процессов уменьшается время расчета. | Показано, что при увеличении количества процессов уменьшается время расчета. | ||
| + | <gallery widths=360px heights=236px perrow = 1> | ||
| + | Файл:Plot_1.jpg | ||
| + | </gallery> | ||
Версия 16:59, 17 января 2016
Постановка задачи
Необходимо вычислить определенный интеграл с использованием средств параллельного программирования на основе MPI.
Реализация
Для расчета указанного интеграла используется метод трапеций - метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подинтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями.
Отрезок [a..b] (в данной задаче [0..1]) разбивается на заданное количество интервалов (в данной задаче n=100000000), и на каждом из элементарных отрезков применяется формула трапеций. Cуммирование даст составную формулу трапеций:
Заданное количество интервалов распределяется между определенным количеством процессов. На каждом полученном таким способом интервале процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы соседние процессы должны обмениваться крайними значениями, полученными на предыдущем шаге, для выполнения следующего шага. Так, каждый процесс рассчитывает определенное количество интервалов по методу трапеций и обменивается информацией с соседними процессами. Суммируя результаты, полученные каждым отдельным процессом, мы получаем конечный результат. Программа, выполняющая расчет интеграла:
Результаты
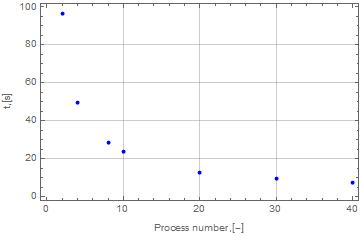
Вычислен определенный интеграл .
Показано, что при увеличении количества процессов уменьшается время расчета.