Одномерное уравнение теплопроводности. Суранов Ян Сергеевич. 6 курс — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Реализация)
(→‎Явная конечно разностная схема)
Строка 18: Строка 18:
  
 
Введем сетку <math>0 < x_i < 1</math> с шагом разбиения <math>Δx</math>. Шаг по времени назовем <math>Δt</math>
 
Введем сетку <math>0 < x_i < 1</math> с шагом разбиения <math>Δx</math>. Шаг по времени назовем <math>Δt</math>
−
Построим явную трехслойную схему:
+
Построим явную конечную разностную схему:
−
:<math>{T_{i}^{n+1}} = {T_{i}^{n-1}}+\frac{2dt}{dx^2}\left(T_{i+1}^{n} - 2T_{i}^{n}+T_{i-1}^{n}\right)</math>
+
:<math>\frac{T_i^{n+1}-T_i^{n}}{Δ t} = \frac{a^2}{Δx^2}\left(T_{i+1}^{n} - 2T_{i}^{n}+T_{i-1}^{n}\right)</math>
 
Где, <math>T_i</math> — значение температуры в <math>i</math>-ом узле.
 
Где, <math>T_i</math> — значение температуры в <math>i</math>-ом узле.
 
Так как схема трехслойная, то вначале надо иметь уже вычисленные значения функции <math>{T_{i}^{n}}</math>  на первом и нулевом слоях.
 
Так как схема трехслойная, то вначале надо иметь уже вычисленные значения функции <math>{T_{i}^{n}}</math>  на первом и нулевом слоях.
  
−
При n=0 значения функции <math>{T_{i}^{0}}</math> определяются из начальных условий. При  значения функции <math>{T_{i}^{1}}</math> вычисляется по двухслойной схеме:
+
 
−
:<math>\frac{T_i^{n+1}-T_i^{n}}{Δ t} = \frac{a^2}{Δx^2}\left(T_{i+1}^{n} - 2T_{i}^{n}+T_{i-1}^{n}\right)</math>
 
 
При <math>{i=0}</math>,<math>{i=1}</math> значения функции определяются из краевых условий.
 
При <math>{i=0}</math>,<math>{i=1}</math> значения функции определяются из краевых условий.
  

Версия 10:59, 15 января 2016

Постановка задачи

Решается однородное уравнение теплопроводности на промежутке [math]\left[0\ldots 1\right][/math]

[math]\frac{\partial T\left(x,t\right)}{\partial t} - k^2\frac{\partial^2 T\left(x,t\right)}{\partial x^2} = f(x,t)[/math]

С граничными условиями

[math] \begin{cases} T(0,t) = T0(t)=cos2t*0.5 \\ T(1,t) = T1(t)=sin2t*0.5 \end{cases}[/math]

и начальным распределением температуры

[math]T(x,0) = T0(x)=10[/math]

Реализация

Явная конечно разностная схема

Задача содержит производную по времени первого порядка и производную по пространственной координате второго порядка. Запишем исходное уравнение в виде:

[math]\frac{\partial T\left(x,t\right)}{\partial t} = a^2\frac{\partial^2 T\left(x,t\right)}{\partial x^2}[/math]

Введем сетку [math]0 \lt x_i \lt 1[/math] с шагом разбиения [math]Δx[/math]. Шаг по времени назовем [math]Δt[/math] Построим явную конечную разностную схему:

[math]\frac{T_i^{n+1}-T_i^{n}}{Δ t} = \frac{a^2}{Δx^2}\left(T_{i+1}^{n} - 2T_{i}^{n}+T_{i-1}^{n}\right)[/math]

Где, [math]T_i[/math] — значение температуры в [math]i[/math]-ом узле. Так как схема трехслойная, то вначале надо иметь уже вычисленные значения функции [math]{T_{i}^{n}}[/math] на первом и нулевом слоях.


При [math]{i=0}[/math],[math]{i=1}[/math] значения функции определяются из краевых условий.

Компьютерная реализация

Скачать программу File:HeatEq_Yan.zip


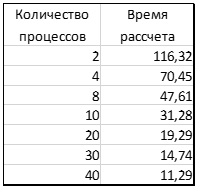
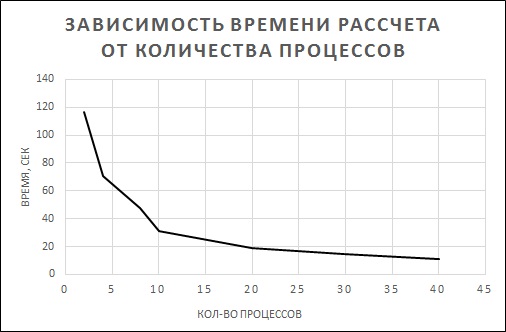
Результаты

Безымянный23.jpg
Безымянный233.jpg
  • При малом числе узлов в сетки, для данной многопроцессовой реализации, время расчета увеличивается.
  • При увеличении числа процессов время расчета существенно сокращается, что делает целесообразным использование данного метода.

Полезные ссылки

Уравнение теплопроводности

Источник — «http://tm.spbstu.ru/?title=Одномерное_уравнение_теплопроводности._Суранов_Ян_Сергеевич._6_курс&oldid=38793»