Одномерное уравнение теплопроводности. Буй Ван Шань. 6 курс — различия между версиями
(→Конечно-разностная схема) |
(→Ссылки для скачивания) |
||
| (не показаны 3 промежуточные версии 1 участника) | |||
| Строка 28: | Строка 28: | ||
Разветвление для уравнения теплопроводности осуществляется путем разбиением отрезка интегрирования на некоторые интервалы. На каждом интервале, процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы, соседние процессы должны обменивать крайними значениями, получены на предыдущем шаге, для выполнения следующего шага. | Разветвление для уравнения теплопроводности осуществляется путем разбиением отрезка интегрирования на некоторые интервалы. На каждом интервале, процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы, соседние процессы должны обменивать крайними значениями, получены на предыдущем шаге, для выполнения следующего шага. | ||
[[File:Sendandreceive.png|Схема передачи данных между процессами|center]] | [[File:Sendandreceive.png|Схема передачи данных между процессами|center]] | ||
| − | : Первый процесс обменивается данными только с процессом | + | : Первый процесс обменивается данными только с вторым процессом |
: Последний процесс обменивается данными только с предпоследним процессом | : Последний процесс обменивается данными только с предпоследним процессом | ||
| − | : Все | + | : Все центральные процессы обмениваются с процессами слево, и справо |
* Начальные и краиние значения на каждом шаге вычисляются по начальным и граничным условиям. | * Начальные и краиние значения на каждом шаге вычисляются по начальным и граничным условиям. | ||
| Строка 80: | Строка 80: | ||
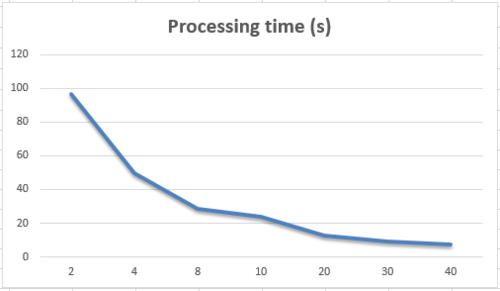
Для малого числа узлов в сетке использовать многопроцессорные вычисления не выгодно: время работы программы неуменьшается. | Для малого числа узлов в сетке использовать многопроцессорные вычисления не выгодно: время работы программы неуменьшается. | ||
Заметим что при увеличении количества процессов, скорость расчета параллельно повысилась | Заметим что при увеличении количества процессов, скорость расчета параллельно повысилась | ||
| − | |||
| − | |||
| − | |||
| − | |||
==Полезные ссылки== | ==Полезные ссылки== | ||
[https://ru.wikipedia.org/wiki/%D0%A3%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D1%82%D0%B5%D0%BF%D0%BB%D0%BE%D0%BF%D1%80%D0%BE%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D1%81%D1%82%D0%B8 Уравнение теплопроводности] | [https://ru.wikipedia.org/wiki/%D0%A3%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D1%82%D0%B5%D0%BF%D0%BB%D0%BE%D0%BF%D1%80%D0%BE%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D1%81%D1%82%D0%B8 Уравнение теплопроводности] | ||
Текущая версия на 22:38, 14 января 2016
Содержание
Постановка задачи[править]
Решается однородное уравнение теплопроводности на промежутке
С граничными условиями
и начальным распределением температуры
- Где : - Известные функции
Реализация[править]
Конечно-разностная схема[править]
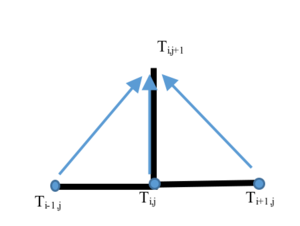
Задача содержит производную по времени первого порядка и производную по пространственной координате второго порядка. Запишем исходное уравнение в виде
Введем равномерную сетку с шагом разбиения . Шаг по времени назовем Построим явную конечно-разностную схему:
Где, — значение температуры в -ом узле.
- Условие сходимости явной схемы:, где dt - шаг по времени, dx - шаг по координате
Применение технологии MPI[править]
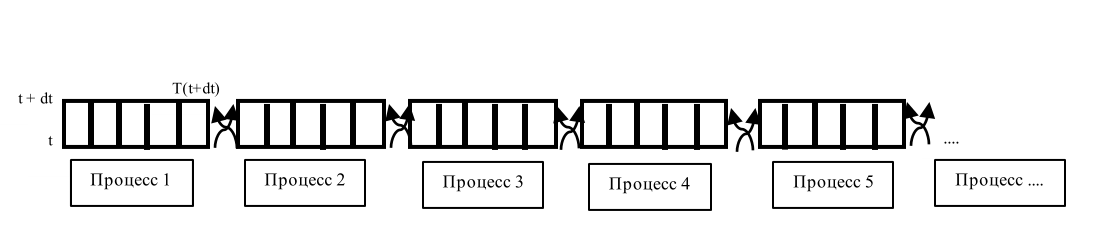
Разветвление для уравнения теплопроводности осуществляется путем разбиением отрезка интегрирования на некоторые интервалы. На каждом интервале, процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы, соседние процессы должны обменивать крайними значениями, получены на предыдущем шаге, для выполнения следующего шага.
- Первый процесс обменивается данными только с вторым процессом
- Последний процесс обменивается данными только с предпоследним процессом
- Все центральные процессы обмениваются с процессами слево, и справо
- Начальные и краиние значения на каждом шаге вычисляются по начальным и граничным условиям.
Данные для расчета[править]
Результаты[править]
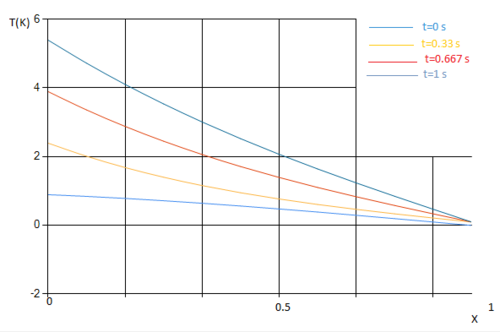
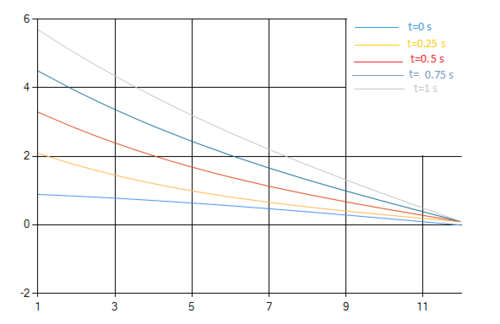
- Решение
- 2 процесса
- 4 процесса
- Погрешность вычисления
- Зависимость времени расчета от количества процессов при постоянных шагах вычисления: dx = 0.001; dt = 0.000001
| Количество процессов | Время рассчета (сек) |
|---|---|
| 2 | 96.58 |
| 4 | 49.4 |
| 8 | 28.66 |
| 10 | 23.63 |
| 20 | 12.89 |
| 30 | 9.27 |
| 40 | 7.52 |
Для малого числа узлов в сетке использовать многопроцессорные вычисления не выгодно: время работы программы неуменьшается. Заметим что при увеличении количества процессов, скорость расчета параллельно повысилась