КП: Моделирование поверхности маятником — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
 
(не показано 7 промежуточных версий 3 участников)
Строка 28: Строка 28:
 
     - движение вдоль осей <math>0x, 0y</math>:
 
     - движение вдоль осей <math>0x, 0y</math>:
  
−
  <math> x = a cos θ + (l + a * θ) sin θ </math>
+
  <math> x = a \cos θ + (l + a θ) \sin θ </math>
−
  <math> y = a sin θ - (l + a * θ) cos θ </math>
+
  <math> y = a \sin θ - (l + a θ) \cos θ </math>
  
 
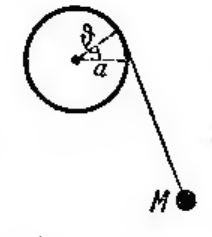
       где  <math> a </math> - радиус цилиндра, <math> l </math> - длина нити, <math> θ </math> - угол отклонения от вертикали
 
       где  <math> a </math> - радиус цилиндра, <math> l </math> - длина нити, <math> θ </math> - угол отклонения от вертикали
Строка 35: Строка 35:
  
 
2. Чтобы реализовать с помощью поступательных движения точки поверхность, размножим эту точку.
 
2. Чтобы реализовать с помощью поступательных движения точки поверхность, размножим эту точку.
−
Предполагается механизм с использованием <math> N </math> маятников ( в нашем случае <math> N = 5</math> ).  
+
Предполагается механизм с использованием <math> N </math> маятников (в нашем случае <math> N = 5</math>).  
 
Удалим маятники друг от друга на расстояние <math> z = a</math> параллельно плоскости <math> 0xy</math>
 
Удалим маятники друг от друга на расстояние <math> z = a</math> параллельно плоскости <math> 0xy</math>
 
Положим <math> (X_i, Y_i, Z_i)</math>, где <math> {i = 1....N}</math>, - позиция каждого маятника.
 
Положим <math> (X_i, Y_i, Z_i)</math>, где <math> {i = 1....N}</math>, - позиция каждого маятника.
 
Для моделирования сложных плоскостей введём параметр длины нити <math> L_i, {i = 1....N}</math> для каждого маятника таким образом, что  
 
Для моделирования сложных плоскостей введём параметр длины нити <math> L_i, {i = 1....N}</math> для каждого маятника таким образом, что  
−
<math> L_i = F (Z_i, l) {i = 1....N}</math> - образует кривую, моделирующею искомую поверхность.  
+
<math> L_i = F (Z_i, l)</math>,  <math>{i = 1....N}</math> - образует кривую, моделирующею искомую поверхность.  
−
Далее в построении простейшей модели будем рассматривать <math> L_i = F (Z_i, l) = l - k * Z^2_i, {i = 1....5} </math>
+
Далее в построении простейшей модели будем рассматривать  
 +
<math> L_i = F (Z_i, l) = l - k Z^2_i </math>, где
 +
<math> {i = 1....5} </math>
  
  
Строка 367: Строка 369:
  
  
 +
</script>
 +
</body>
 +
</html>
 +
</syntaxhighlight>
 
</div>
 
</div>
  
Строка 373: Строка 379:
 
[[Файл:Efremresults.JPG]]
 
[[Файл:Efremresults.JPG]]
  
−
Данная работа демонстрирует возможности моделирования сложных поверхностей ( плоскостей, вырезов, отливов и т.д.)  исходя из комбинаций движения точек по законам классической механики.  
+
Данная работа демонстрирует возможности моделирования сложных поверхностей (плоскостей, вырезов, отливов и т.д)  исходя из комбинаций движения точек по законам классической механики.  
 
<br>
 
<br>
  

Текущая версия на 18:24, 16 декабря 2015

А.М. Кривцов > Теоретическая механика > Курсовые проекты ТМ 2015 > Моделирование поверхности маятником

Foucault pendulum animated.gif

Курсовой проект по Теоретической механике

Исполнитель: Ефремов Дмитрий

Группа: 09 (23604)

Семестр: весна 2015

Аннотация проекта[править]

Данный проект посвящен изучению возможностей моделирования сложных поверхностей с помощью маятников переменной длины.

Формулировка задачи[править]

Написать программу, представляющею простейший механизм на основе движения маятника, для моделирования сложных поверхностей.

Общие сведения по теме[править]

Нить намотана на неподвижный цилиндр (a — радиус цилиндра), Рассматриваемый угол θ - есть угол отклонения от вертикали.

Маятник переменной длины — основной инструмент в решении представленной задачи. Основным его свойством является изменение длины нерастяжимой нити по ходу движения маятника согласно определенному закону. По механическим параметрам подобная система схожа с математическим маятником.


Решение[править]

1. Изучение движения исследуемого маятника.

    - движение вдоль осей [math]0x, 0y[/math]:

[math] x = a \cos θ + (l + a  θ) \sin θ [/math]
[math] y = a \sin θ - (l + a  θ) \cos θ [/math]

      где  [math] a [/math] - радиус цилиндра, [math] l [/math] - длина нити, [math] θ [/math] - угол отклонения от вертикали


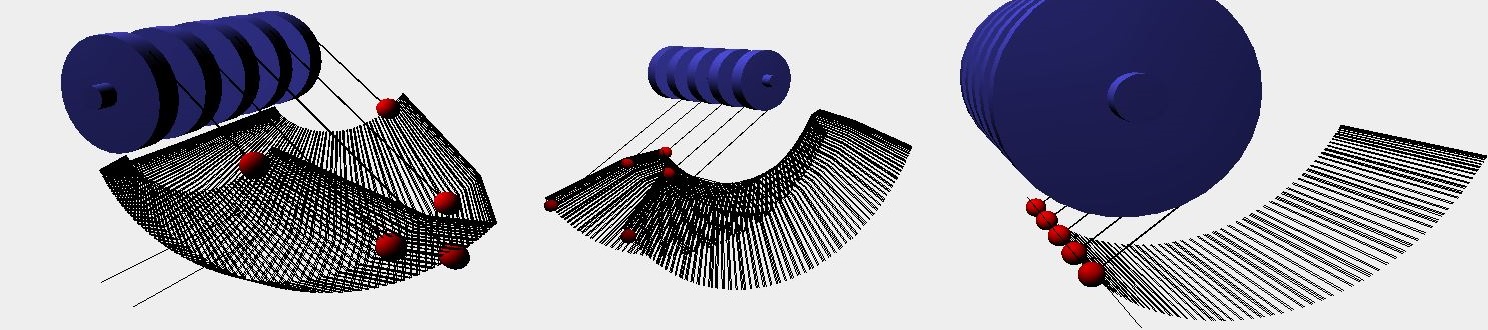
2. Чтобы реализовать с помощью поступательных движения точки поверхность, размножим эту точку. Предполагается механизм с использованием [math] N [/math] маятников (в нашем случае [math] N = 5[/math]). Удалим маятники друг от друга на расстояние [math] z = a[/math] параллельно плоскости [math] 0xy[/math] Положим [math] (X_i, Y_i, Z_i)[/math], где [math] {i = 1....N}[/math], - позиция каждого маятника. Для моделирования сложных плоскостей введём параметр длины нити [math] L_i, {i = 1....N}[/math] для каждого маятника таким образом, что [math] L_i = F (Z_i, l)[/math], [math]{i = 1....N}[/math] - образует кривую, моделирующею искомую поверхность. Далее в построении простейшей модели будем рассматривать [math] L_i = F (Z_i, l) = l - k Z^2_i [/math], где [math] {i = 1....5} [/math]


3. Зафиксируем угол качения, исходную длину маятника [math] l = 20, |θ| \lt π/6 [/math] и смоделируем процесс:

Текст программы на языке JavaScript:

Файл "Nano_kl.js" 

  1 function main()
  2 {
  3 	var step = 0;
  4 	var stats = initStats();
  5 	var i = 0;
  6 
  7 	//определяем сцену
  8 
  9 	var material = new THREE.LineBasicMaterial({color: 0x000000});
 10 	
 11 	var scene = new THREE.Scene();
 12 	var camera = new THREE.PerspectiveCamera(45, window.innerWidth/window.innerHeight, 0.1, 10000);
 13 	var render = new THREE.WebGLRenderer();
 14 	render.setClearColor(0xEEEEEE);
 15 	render.setSize(window.innerWidth ,window.innerHeight-80);
 16 	
 17 	//ставим оси
 18 	
 19 	var axes = new THREE.AxisHelper(1);
 20 	scene.add(axes);
 21 	var planeGeometry = new THREE.PlaneGeometry(60, 20, 1, 1);
 22 	var planeMaterial = new THREE.MeshLambertMaterial({color:0xcccccc});
 23 	var plane = new THREE.Mesh(planeGeometry,planeMaterial);
 24 	plane.rotation.x = -0.5*Math.PI;
 25 	plane.position.x = 15;
 26 	plane.position.y = 0;
 27 	plane.position.z = 0;
 28 	
 29 	var cylinderGeometry = new THREE.CylinderGeometry(1,1,25,32);
 30 	var cylinderMaterial = new THREE.MeshLambertMaterial({color:0x5555f1, wireframe:false});
 31 	var vint = new THREE.Mesh(cylinderGeometry, cylinderMaterial);
 32 	vint.position.x = 0;	vint.position.y = 0;	vint.position.z = 0;
 33 	vint.rotation.x = 0.5*Math.PI;
 34 	scene.add(vint);
 35 
 36 	
 37 	//создаем ШАРИК
 38 	var cubeGeometry = new THREE.SphereGeometry(1,20,20);
 39 	var cubeMaterial = new THREE.MeshLambertMaterial({color:0xff0000, wireframe:false});
 40 	var cube = new THREE.Mesh(cubeGeometry, cubeMaterial);
 41 	cube.position.x = 0;	cube.position.y = -20;	cube.position.z = 0;
 42 	scene.add(cube);
 43 	// создаем нитку
 44 	var cubeGeometry = new THREE.CubeGeometry(0.1,20,0.1);
 45 	var cubeMaterial = new THREE.MeshLambertMaterial({color:0x000000, wireframe:false});
 46 	var cube3 = new THREE.Mesh(cubeGeometry, cubeMaterial);
 47 	cube3.position.x = 5;	cube3.position.y = -10;	cube3.position.z = 0;
 48 	cube3.rotation.x = 0;	cube3.rotation.y = 0;	cube3.rotation.z = 0;
 49 	scene.add(cube3);
 50 	//создаем цилиндр
 51 	var cylinderGeometry = new THREE.CylinderGeometry(5,5,2,32);
 52 	var cylinderMaterial = new THREE.MeshLambertMaterial({color:0x5555f1, wireframe:false});
 53 	var cylinder = new THREE.Mesh(cylinderGeometry, cylinderMaterial);
 54 	cylinder.position.x = 0;	cylinder.position.y = 0;	cylinder.position.z = 0;
 55 	cylinder.rotation.x = 0.5*Math.PI;
 56 	scene.add(cylinder);
 57 	
 58 	//создаем ШАРИК
 59 	var cubeGeometry = new THREE.SphereGeometry(1,20,20);
 60 	var cubeMaterial = new THREE.MeshLambertMaterial({color:0xff0000, wireframe:false});
 61 	var cube_1 = new THREE.Mesh(cubeGeometry, cubeMaterial);
 62 	cube_1.position.x = 0;	cube_1.position.y = -20;	cube_1.position.z = 5;
 63 	scene.add(cube_1);
 64 	// создаем нитку
 65 	var cubeGeometry = new THREE.CubeGeometry(0.1,20,0.1);
 66 	var cubeMaterial = new THREE.MeshLambertMaterial({color:0x000000, wireframe:false});
 67 	var cube3_1 = new THREE.Mesh(cubeGeometry, cubeMaterial);
 68 	cube3_1.position.x = 5;	cube3_1.position.y = -10;	cube3_1.position.z = 5;
 69 	cube3_1.rotation.x = 0;	cube3_1.rotation.y = 0;	cube3_1.rotation.z = 0;
 70 	scene.add(cube3_1);
 71 	//создаем цилиндр
 72 	var cylinderGeometry = new THREE.CylinderGeometry(5,5,2,32);
 73 	var cylinderMaterial = new THREE.MeshLambertMaterial({color:0x5555f1, wireframe:false});
 74 	var cylinder_1 = new THREE.Mesh(cylinderGeometry, cylinderMaterial);
 75 	cylinder_1.position.x = 0;	cylinder_1.position.y = 0;	cylinder_1.position.z = 5;
 76 	cylinder_1.rotation.x = 0.5*Math.PI;
 77 	scene.add(cylinder_1);
 78 	
 79 		//создаем ШАРИК
 80 	var cubeGeometry = new THREE.SphereGeometry(1,20,20);
 81 	var cubeMaterial = new THREE.MeshLambertMaterial({color:0xff0000, wireframe:false});
 82 	var cube_2 = new THREE.Mesh(cubeGeometry, cubeMaterial);
 83 	cube_2.position.x = 0;	cube_2.position.y = -20;	cube_2.position.z = 10;
 84 	scene.add(cube_2);
 85 	// создаем нитку
 86 	var cubeGeometry = new THREE.CubeGeometry(0.1,20,0.1);
 87 	var cubeMaterial = new THREE.MeshLambertMaterial({color:0x000000, wireframe:false});
 88 	var cube3_2 = new THREE.Mesh(cubeGeometry, cubeMaterial);
 89 	cube3_2.position.x = 5;	cube3_2.position.y = -10;	cube3_2.position.z = 10;
 90 	cube3_2.rotation.x = 0;	cube3_2.rotation.y = 0;	cube3_2.rotation.z = 0;
 91 	scene.add(cube3_2);
 92 	//создаем цилиндр
 93 	var cylinderGeometry = new THREE.CylinderGeometry(5,5,2,32);
 94 	var cylinderMaterial = new THREE.MeshLambertMaterial({color:0x5555f1, wireframe:false});
 95 	var cylinder_2 = new THREE.Mesh(cylinderGeometry, cylinderMaterial);
 96 	cylinder_2.position.x = 0;	cylinder_2.position.y = 0;	cylinder_2.position.z = 10;
 97 	cylinder_2.rotation.x = 0.5*Math.PI;
 98 	scene.add(cylinder_2);
 99 	
100 	//создаем ШАРИК
101 	var cubeGeometry = new THREE.SphereGeometry(1,20,20);
102 	var cubeMaterial = new THREE.MeshLambertMaterial({color:0xff0000, wireframe:false});
103 	var cube_4 = new THREE.Mesh(cubeGeometry, cubeMaterial);
104 	cube_4.position.x = 0;	cube_4.position.y = -20;	cube_4.position.z = -5;
105 	scene.add(cube_4);
106 	// создаем нитку
107 	var cubeGeometry = new THREE.CubeGeometry(0.1,20,0.1);
108 	var cubeMaterial = new THREE.MeshLambertMaterial({color:0x000000, wireframe:false});
109 	var cube3_4 = new THREE.Mesh(cubeGeometry, cubeMaterial);
110 	cube3_4.position.x = 5;	cube3_4.position.y = -10;	cube3_4.position.z = -5;
111 	cube3_4.rotation.x = 0;	cube3_4.rotation.y = 0;	cube3_4.rotation.z = 0;
112 	scene.add(cube3_4);
113 	//создаем цилиндр
114 	var cylinderGeometry = new THREE.CylinderGeometry(5,5,2,32);
115 	var cylinderMaterial = new THREE.MeshLambertMaterial({color:0x5555f1, wireframe:false});
116 	var cylinder_4 = new THREE.Mesh(cylinderGeometry, cylinderMaterial);
117 	cylinder_4.position.x = 0;	cylinder_4.position.y = 0;	cylinder_4.position.z = -5;
118 	cylinder_4.rotation.x = 0.5*Math.PI;
119 	scene.add(cylinder_4);
120 	
121 		//создаем ШАРИК
122 	var cubeGeometry = new THREE.SphereGeometry(1,20,20);
123 	var cubeMaterial = new THREE.MeshLambertMaterial({color:0xff0000, wireframe:false});
124 	var cube_5 = new THREE.Mesh(cubeGeometry, cubeMaterial);
125 	cube_5.position.x = 0;	cube_5.position.y = -20;	cube_5.position.z = -10;
126 	scene.add(cube_5);
127 	// создаем нитку
128 	var cubeGeometry = new THREE.CubeGeometry(0.1,20,0.1);
129 	var cubeMaterial = new THREE.MeshLambertMaterial({color:0x000000, wireframe:false});
130 	var cube3_5 = new THREE.Mesh(cubeGeometry, cubeMaterial);
131 	cube3_5.position.x = 5;	cube3_5.position.y = -10;	cube3_5.position.z = -10;
132 	cube3_5.rotation.x = 0;	cube3_5.rotation.y = 0;	cube3_5.rotation.z = 0;
133 	scene.add(cube3_5);
134 	//создаем цилиндр
135 	var cylinderGeometry = new THREE.CylinderGeometry(5,5,2,32);
136 	var cylinderMaterial = new THREE.MeshLambertMaterial({color:0x5555f1, wireframe:false});
137 	var cylinder_5 = new THREE.Mesh(cylinderGeometry, cylinderMaterial);
138 	cylinder_5.position.x = 0;	cylinder_5.position.y = 0;	cylinder_5.position.z = -10;
139 	cylinder_5.rotation.x = 0.5*Math.PI;
140 	scene.add(cylinder_5);
141 	
142 	
143 	// устанавливаем источник света
144 	
145 	var spotLight = new THREE.SpotLight(0xffffff);
146 	spotLight.position.set(-40,60,40);
147 	scene.add(spotLight);
148 	
149 	
150 	var geometry = new THREE.Geometry();
151     geometry.vertices.push(new THREE.Vector3(0, 0, 2.51));
152     geometry.vertices.push(new THREE.Vector3(-4,0,2.51));
153 	
154 	var line = new THREE.Line(geometry, material);
155 	line.geometry.verticesNeedUpdate = true;
156 	geometry.dynamic = true;
157 	
158 	scene.add(line);
159 	//задаем тени
160 	
161 	render.shadowMapEnabled = true;
162 	plane.receiveShadow = true;
163 	cube.castShadow = true;
164 	spotLight.castShadow = true;
165 	
166 	//задаем положение камеры
167 	camera.position.x =0;
168 	camera.position.y = 0;
169 	camera.position.z = 60;
170 	camera.lookAt(scene.position);
171 	$("#webGL").append(render.domElement);
172 	
173 	//добавляем ползунки для настройки скорости вращения и радиуса цилиндра
174 		var controls = new function()
175 		{
176 			this.rotationSpeed = 0.5;
177 			this.bouncingSpeed = 0.03;
178 			this.radius = 1;	
179 		}
180 	
181 	var gui = new dat.GUI();
182 	gui.add(controls,'rotationSpeed',0,1);
183 	gui.add(controls,'radius',0,2);
184 	
185 	
186 	
187 	
188 	ccontrols = new THREE.OrbitControls(camera);
189 
190 
191 	
192 
193 
194 	
195 	
196 	renderer();	
197 	
198 	// функция, в уоторой задаются законы, по которым работает кривошипно0шатунный механизм
199 function renderer()
200 {
201 	stats.update();
202 	// Связываем бегунок и частоту колебаний
203 	//cylinder.rotation.y -=controls.rotationSpeed;
204 	
205 	// Вводим расчётные данные 
206 	step += -0.02;
207 	i += 1;
208 	fi = Math.PI * Math.sin(step) / 3;
209 	co  = Math.cos(fi);
210 	si = Math.sin(fi);
211 	a = 5 * controls.radius;
212 	l = 20;
213 	l_5 = l - (16*Math.cos(Math.PI*controls.rotationSpeed));
214 	l_4 = l - (4*Math.cos(Math.PI*controls.rotationSpeed));
215 	// Задаём траекторию движения щарика
216 	cube.position.y =  ( a * (si) - (20 + a * fi ) * (co) );
217 	cube.position.x =  ( a * (co) + (20 + a * fi ) * (si) ) ;
218 	cube3.position.y = ( a * (si) - (20 + a * fi ) / 2 * (co) );
219 	cube3.position.x = ( a * (co) + (20 + a * fi ) / 2 * (si) );
220 	
221 	cube_4.position.y =  cube_1.position.y = ( a * (si) - (l_4 + a * fi ) * (co) );
222 	cube_4.position.x = cube_1.position.x =  ( a * (co) + (l_4 + a * fi ) * (si) );
223 	cube3_4.position.y = cube3_1.position.y = ( a * (si) - (l_4 + a * fi ) / 2 * (co) );
224 	cube3_4.position.x =  cube3_1.position.x = ( a * (co) + (l_4 + a * fi ) / 2 * (si) );
225 	
226 	cube_5.position.y = cube_2.position.y = ( a * (si) - (l_5 + a * fi ) * (co) );
227 	cube_5.position.x = cube_2.position.x = ( a * (co) + (l_5 + a * fi ) * (si) ) ;
228 	cube3_5.position.y = cube3_2.position.y = ( a * (si) - (l_5 + a * fi ) / 2 * (co) );
229 	cube3_5.position.x = cube3_2.position.x = ( a * (co) + (l_5 + a * fi ) / 2 * (si) );
230 	
231 	cube3_5.rotation.z = cube3_4.rotation.z = cube3_2.rotation.z = cube3_1.rotation.z = cube3.rotation.z = fi;
232 	
233 	// Задаём движение нити	
234 	 
235 	
236 	
237 	cube3.scale.set(1, (1 + a * fi / 20),1);
238 	cube3_1.scale.set(1, (l_4 / 20)*(1 + a * fi / l_4),1);
239 	cube3_2.scale.set(1, (l_5 / 20)*(1 + a * fi / l_5),1);
240 	cube3_4.scale.set(1, (l_4 / 20)*(1 + a * fi / l_4),1);
241 	cube3_5.scale.set(1, (l_5 / 20)*(1 + a * fi / l_5),1);
242 	
243 	
244 	
245 	// Связь данных настраеваемых ползунками с общей программой
246 	cylinder.scale.set(controls.radius,1,controls.radius);	
247 	cylinder_1.scale.set(controls.radius,1,controls.radius);
248 	cylinder_2.scale.set(controls.radius,1,controls.radius);
249 	cylinder_4.scale.set(controls.radius,1,controls.radius);
250 	cylinder_5.scale.set(controls.radius,1,controls.radius);
251 	vint.scale.set(controls.radius,1,controls.radius);
252 	
253 	
254 	// Рисуем след после шарика
255 	var lineGeometry = new THREE.Geometry();
256 	lineGeometry.vertices.push(new THREE.Vector3(cube_5.position.x, cube_5.position.y, -10));
257 	lineGeometry.vertices.push(new THREE.Vector3(cube_4.position.x, cube_4.position.y, -5));
258 	lineGeometry.vertices.push(new THREE.Vector3(cube.position.x, cube.position.y, 0));
259 	lineGeometry.vertices.push(new THREE.Vector3(cube_1.position.x, cube_1.position.y, 5));
260 	lineGeometry.vertices.push(new THREE.Vector3(cube_2.position.x, cube_2.position.y, 10));
261 	var lineMaterial = new THREE.LineBasicMaterial({color:0x000000, linewidth: 1}); 
262 	var line = new THREE.Line(lineGeometry, lineMaterial);
263 	if ( i == 10 )
264 	{
265 	scene.add(line);
266 	i = 0;
267 	}
268 	/*
269 	lineGeometry.vertices.push(new THREE.Vector3(cube_1.position.x, cube_1.position.y, 5));
270 	lineGeometry.vertices.push(new THREE.Vector3(cube_1.position.x + 0.1, cube_1.position.y + 0.1, 5));
271 	var lineMaterial = new THREE.LineBasicMaterial({color:0x000000, linewidth:5000}); 
272 	var line_1 = new THREE.Line(lineGeometry, lineMaterial);
273 	scene.add(line_1);
274 	
275 	lineGeometry.vertices.push(new THREE.Vector3(cube_2.position.x, cube_2.position.y, 10));
276 	lineGeometry.vertices.push(new THREE.Vector3(cube_2.position.x + 0.1, cube_2.position.y + 0.1, 10));
277 	var lineMaterial = new THREE.LineBasicMaterial({color:0x000000, linewidth:5000}); 
278 	var line_2 = new THREE.Line(lineGeometry, lineMaterial);
279 	scene.add(line_2);
280 	
281 	lineGeometry.vertices.push(new THREE.Vector3(cube_4.position.x, cube_4.position.y, -5));
282 	lineGeometry.vertices.push(new THREE.Vector3(cube_4.position.x + 0.1, cube_4.position.y + 0.1, -5));
283 	var lineMaterial = new THREE.LineBasicMaterial({color:0x000000, linewidth:5000}); 
284 	var line_4 = new THREE.Line(lineGeometry, lineMaterial);
285 	scene.add(line_4);
286 	
287 	lineGeometry.vertices.push(new THREE.Vector3(cube_5.position.x, cube_5.position.y, -10));
288 	lineGeometry.vertices.push(new THREE.Vector3(cube_5.position.x + 0.1, cube_5.position.y + 0.1, -10));
289 	var lineMaterial = new THREE.LineBasicMaterial({color:0x000000, linewidth:5000}); 
290 	var line_5 = new THREE.Line(lineGeometry, lineMaterial);
291 	scene.add(line_5);
292 	*/
293 	
294 	
295 	requestAnimationFrame(renderer);
296 	ccontrols.update();
297 	document.getElementById("td1").innerHTML = cube3.rotation.z ;	//даные, который будут выведены в таблицу
298 	document.getElementById("td2").innerHTML = cube.position.y ;
299 	render.render(scene, camera);
300 	
301 }
302 }
303 
304 function initStats()
305 {
306 	var stats = new Stats();
307 	stats.setMode(0);
308 	stats.domElement.style.position = 'absolute';
309 	stats.domElement.style.left = '0px';
310 	stats.domElement.style.top = '0px';
311 	$("#stats").append(stats.domElement);
312 	return stats;
313 }
314 
315 
316 
317 </script>
318 </body>
319 </html>

Обсуждение результатов и выводы[править]

Efremresults.JPG

Данная работа демонстрирует возможности моделирования сложных поверхностей (плоскостей, вырезов, отливов и т.д) исходя из комбинаций движения точек по законам классической механики.

Ссылки по теме[править]

См. также[править]

Источник — «http://tm.spbstu.ru/?title=КП:_Моделирование_поверхности_маятником&oldid=38285»