Моделирование упругого стержня на примере позвоночника — различия между версиями
| (не показана 21 промежуточная версия 2 участников) | |||
| Строка 14: | Строка 14: | ||
== Постановка задачи: Модель == | == Постановка задачи: Модель == | ||
| + | [[File:Sravn2.png|thumbnail|Нагрузка от мышц]] | ||
| + | [[File:Sravn.png|thumbnail|Распределенная нагрузка в результате давления руюкзака]] | ||
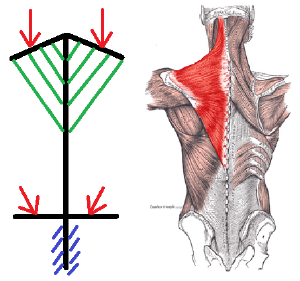
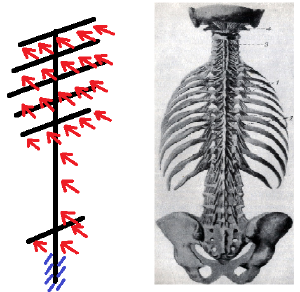
* Нагрузка от лямок передается по абсолютно упругим пружинам – мышцам в виде распределенной нагрузки на позвоночник | * Нагрузка от лямок передается по абсолютно упругим пружинам – мышцам в виде распределенной нагрузки на позвоночник | ||
* Точечные силы и моменты от сил, действующих на ребра и на таз | * Точечные силы и моменты от сил, действующих на ребра и на таз | ||
| Строка 20: | Строка 22: | ||
== Постановка задачи: Уравнения == | == Постановка задачи: Уравнения == | ||
* Уравнения статики | * Уравнения статики | ||
| − | < | + | Усилие в позвоночнике<br> |
| − | + | <math> \dot N \ =\ {f_{n}\left(s\right)} + {f_{m}\left(s\right)} + {f_{i}\delta\left(s_{i}\right)}</math><br> | |
| − | == | + | Момент в позвоночнике<br> |
| − | + | <math> \dot M \ + j\times N =\ {m_{i}\delta\left(s_{i}\right)}</math><br> | |
| + | <br> | ||
| + | * Векторы деформации и внутренняя энергия | ||
| + | Вектор растяжения-поперечного сдвига<br> | ||
| + | <math>e = \dot U\ + j\times \Psi </math><br> | ||
| + | Вектор изгиба-кручения<br> | ||
| + | <math>k = \dot \Psi\ </math><br> | ||
| + | Внутренняя энергия<br> | ||
| + | <math>\rho_{0}U = \frac{1}{2}e*A*e + \frac{1}{2}k*C*k </math><br> | ||
== Точное решение== | == Точное решение== | ||
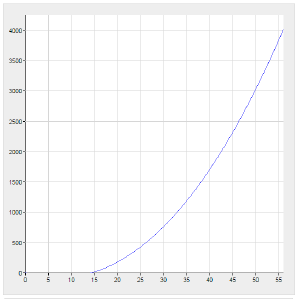
| + | * Изгиб позвоночника | ||
| + | [[File:Izgib.png|thumbnail|Изгиб позвоночника]] | ||
| + | <math>\Psi_{z} = {\frac{N_{позв}}{C_{z}}} {\frac{s^3}{6}} + ({\frac{s^2}{2}} - s_{i}s)\Sigma(N_{таза}-F_{пояса}+N_{ребра_{i}})*H(s-s_{i}) </math> | ||
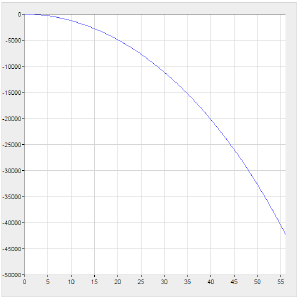
| + | * Деформации по x | ||
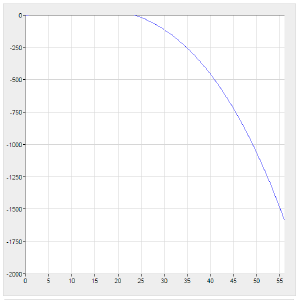
| + | [[File:Deformx.png|thumbnail|Деформации позвоночника по х]] | ||
| + | <math>U_{x} = -{\frac{N_{позв}}{C_{z}}} {\frac{s^4}{24}} - ({\frac{s^3}{6}} - s_{i}{\frac{s^2}{2}})\Sigma(N_{таза}-F_{пояса}+N_{ребра_{i}})*H(s-s_{i}) </math> | ||
| − | + | * Деформации по y | |
| − | + | [[File:Deformy.png|thumbnail|Деформации позвоночника по у]] | |
| − | + | <math>U_{y} = {\frac{2F_{лямок}}{A_{y}a^2}} {\frac{s^3}{6}} - {\frac{N_{0}}{A_{y}}}s + {\frac{F_{пояса}}{A_{y}}}H(s-s_{i}) </math> | |
| − | = | ||
| − | |||
== Выводы == | == Выводы == | ||
| − | * | + | * На основе линейной теории стержней разработана модель по определению нагрузок со стороны рюкзака. |
| − | + | * Получена зависимость изгиба и деформаций стержня от управляющих параметров | |
| − | * | + | * Обнаружено, что: |
| − | + | ** Деформации позвоночника U будут уменьшаться с увеличением угла поясника β | |
| − | * | + | ** Уменьшить изгиб позвоночника Ψ мы можем расположив центр масс как можно ближе к тазу |
| − | |||
| − | * | ||
== Список литературы == | == Список литературы == | ||
| − | 1. | + | 1. «Прикладная механика. Теория тонких упругих стержней» П.А. Жилин, 2007 г<br> |
| − | + | 2. «Медицинская и биологическая физика. Курс лекций с задачами: учеб. Пособие» В.Н. Федорова, Е.В. Фаустов, 2008 г<br> | |
| − | 2. | + | 3. Journal of Biomechanics 33 (2000) 881-888<br> |
| − | + | 4. «Хирургия позвоночника» 2/2006 © А.И. Продан и др.<br> | |
| − | 3. | ||
| − | |||
| − | 4. | ||
Текущая версия на 13:23, 30 ноября 2015
Содержание
Руководитель[править]
Вильчевская Е.Н.
Введение[править]
В работе рассматривается частный случай гибкого стержня – позвоночник человека. Грамотная нагрузка позвоночника важна как в детстве – при большой гибкости и постоянных изменениях размеров позвоночника, так и в дальнейшем, когда приходится выбирать что носить – рюкзак или сумку, или при экстремальных нагрузках в походах. В дальнейшем результаты работы позволят составить общую теорию по оптимальной нагрузке позвоночника. А так же могут послужить подсказкой к оптимальной нагрузке гибких стержней в целом. Так же данная тема позволяет мне продемонстрировать умение строить математические модели, что является целью моего обучения в бакалавриате по данной специальности. Целью данной работы является возможность доказать, что правильная нагрузка на позвоночник может существенно снизить его деформации. Я рассчитала деформации и изгибы сечений стержня для наиболее часто встречающихся параметров.
Цели[править]
- Смоделировать нагрузки на стержень
- Рассчитать численно силы, действующие на позвоночник
- Составить формулы для векторов деформации и изгиба позвоночника
- Выявить зависимость деформаций и изгиба позвоночника в зависимости от управляющих параметров
Постановка задачи: Модель[править]
- Нагрузка от лямок передается по абсолютно упругим пружинам – мышцам в виде распределенной нагрузки на позвоночник
- Точечные силы и моменты от сил, действующих на ребра и на таз
- Распределенная сила, действующая в позвоночнике в результате давления рюкзака на позвоночник
Постановка задачи: Уравнения[править]
- Уравнения статики
Усилие в позвоночнике
Момент в позвоночнике
- Векторы деформации и внутренняя энергия
Вектор растяжения-поперечного сдвига
Вектор изгиба-кручения
Внутренняя энергия
Точное решение[править]
- Изгиб позвоночника
- Деформации по x
- Деформации по y
Выводы[править]
- На основе линейной теории стержней разработана модель по определению нагрузок со стороны рюкзака.
- Получена зависимость изгиба и деформаций стержня от управляющих параметров
- Обнаружено, что:
- Деформации позвоночника U будут уменьшаться с увеличением угла поясника β
- Уменьшить изгиб позвоночника Ψ мы можем расположив центр масс как можно ближе к тазу
Список литературы[править]
1. «Прикладная механика. Теория тонких упругих стержней» П.А. Жилин, 2007 г
2. «Медицинская и биологическая физика. Курс лекций с задачами: учеб. Пособие» В.Н. Федорова, Е.В. Фаустов, 2008 г
3. Journal of Biomechanics 33 (2000) 881-888
4. «Хирургия позвоночника» 2/2006 © А.И. Продан и др.