Одномерное уравнение теплопроводности. Буй Ван Шань. 6 курс — различия между версиями

Версия 23:21, 18 ноября 2015

Постановка задачи

Пример численного решения уравнения теплопроводности. Цветом и высотой поверхности передана температура данной точки.

Решается однородное уравнение теплопроводности на промежутке [math]\left[a\ldots b\right][/math]

[math]\frac{\partial U\left(x,t\right)}{\partial t} - k^2\frac{\partial^2 U\left(x,t\right)}{\partial x^2} = f(x,t)[/math]

С граничными условиями

[math] \begin{cases} U(a,t) = M1(t) \\ U(b,t) = M2(t) \end{cases}[/math]

и начальным распределением температуры

[math]U(x,0) = U0(x)[/math]

• Где :[math]f(x,t), U0(x), M1(t), M2(t)[/math] - Известные функции

Реализация

• Данные для расчета

[math] \begin{cases} a=0;b=1\\ M1(t)=6t+0.887\\ M2(t)=0.0907\\ U0(x)=cos(x+0.48)\\ f(x,t)=0\\ k=1 \end{cases}[/math]

• Скачать Файл:HeatEquation.rar

Результаты

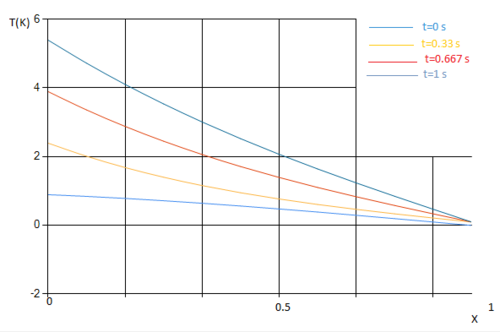
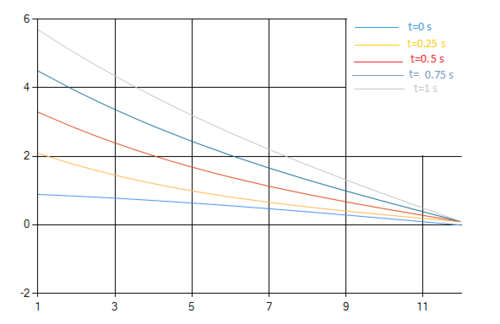
• Решение
  • 2 процесса

Решение при запуске 2-х процессов

• 4 процесса

Решение при запуске 4-х процессов

• Погрешность вычисления
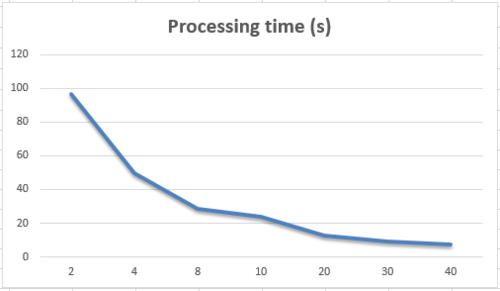
• Зависимость времени расчета от количества процессов при постоянных шагах вычисления: dx = 0.001; dt = 0.000001

Зависимость времени расчета от кол. процессов

!Количество процессов !Время рассчета (сек) |- |2 |96.58 |- |4 |49.4 |- |8 |28.66 |- |10 |23.63 |- |20 |12.89 |- |30 |9.27 |- |40 | 7.52 |} Заметим что при запуске больше количества процессов, скорость расчета быстро снижается