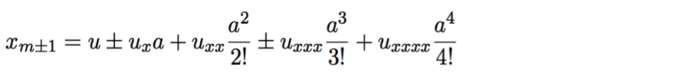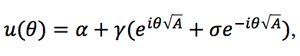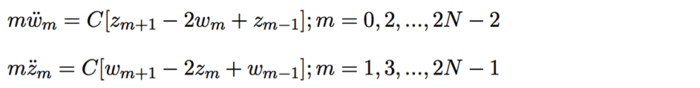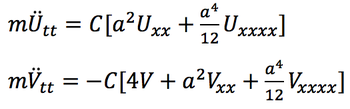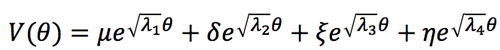Линейные плоские волны в материале с квадратной решёткой. — различия между версиями
Алёна (обсуждение | вклад) (→Двухполевая модель) |
Алёна (обсуждение | вклад) |
||
| Строка 52: | Строка 52: | ||
| + | =Двухполевая модель= | ||
| − | = | + | ==Неустойчивая решётка== |
*Дискретные уравнение движения: | *Дискретные уравнение движения: | ||
| Строка 63: | Строка 64: | ||
*Получившееся решение (решение для u аналогично решению уравнения однополевой модели): | *Получившееся решение (решение для u аналогично решению уравнения однополевой модели): | ||
[[Файл:solut2.png|500px]] | [[Файл:solut2.png|500px]] | ||
| + | |||
| + | ==Устойчивая решётка== | ||
=Выводы= | =Выводы= | ||
Текущая версия на 00:18, 25 октября 2015
Содержание
Руководитель[править]
доц. к. ф.-м. н. Беринский И.Е.
Введение[править]
Исследования в области описания динамики распространения плоских волн в различных кристаллических решётках связаны, в первую очередь, с именем М.Борна, чьи работы датируются началом XX века и не теряют актуальности и по сей день в связи с развитием нанотехнологий и наноэлектроники. Так, задача о распространении линейной волны в одномерной моноатомной цепочке является классической. Модификации этой задачи, а также её обобщения на двумерные решётки рассматривались множеством учёных.
Необходимость построения многополевых моделей при описании распространения волн обусловлена тем, что при континуальном описании не учитываются физические эффекты, связанные с внутренней структурой материала. Построение подобных моделей даст возможность рассматривать системы с учётом информации структурного уровня, не отказываясь при этом от преимуществ континуальных моделей: например, двухполевая модель, в отличие от однополевой, позволяет рассматривать короткие волны.
При построении многополевых моделей дополнительно к полю перемещений для описания изменений, происходящих в рассматриваемой решётке/структуре вводятся системы нескольких взаимопроникающих полей. Для этого выбирается макроячейка моделируемой системы. В зависимости от того, какую модель необходимо построить, выбирается либо минимальная ячейка периодичности (в случае однополевой модели), либо, в случае многополевого подхода, базовая ячейка периодичности может включать несколько элементарных. Особенностью многополевого подхода является то, что, несмотря на идентичность частиц, решётка разбивается на N взаимопроникающих подрешёток, которые маркируются индексами от 1 до N, где N-количество полей.
Актуальность построения подобных моделей для различных, в частности, квадратных, кристаллических решёток, состоит в желании описывать свойства материалов, которые в массе своей синтезируются искуственно – метаматериалов.
Метаматериалы выделены в отдельный класс материалов, так как их свойства зависят от структуры компонентов, упорядоченных особым образом, и могут кардинально отличаться от свойств составляющих их компонентов. Существуют метаматериалы с многократно увеличенными электрической проницаемостью и магнитной восприимчивостью, метаматериалы, эффективность нелинейных эффектов в которых увеличивается на много порядков по сравнению с обычными веществами. Примером могут послужить ауксетики, обладающие полезными механическими свойствами, такими как значительное поглощение механической энергии и высокое сопротивление разрушению.
Хотя возможность управления структурой компонентов материала дает новую степень свободы в конструировании их свойств, однако настоящую революцию произвели работы, продемонстрировавшие возможность создания метаматериалов со свойствами, которые не встречаются в природных материалах. Например, с отрицательным коэффициентом преломления, у которых одновременно отрицательны диэлектрическая и магнитная проницаемости.
Для описания распространения волн в подобных материалах могут использоваться построенные в данной работе модели.
Цели и задачи работы[править]
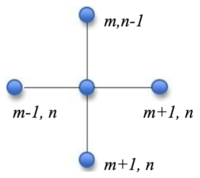
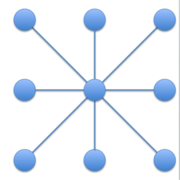
- Целью данной работы является описание динамики плоских волн в материале, который на микроуровне представляет собой квадратную решётку с одинаковым типом частиц. Рассматриваются квадратные решётки (Рис.1, 2), для которой уже были получены уравнения движения.
Были решены задачи построения однополевых и многополевых (двух- и четырёхполевых) моделей для обеих решёток.
Общие соображения[править]
Дисперсионный анализ позволяет выделить 2 разных спектра колебаний частиц, высокочастотный и низкочастотный. В случае низкочастотных колебаний все частицы на графике зависимости перемещения от времени лежат на одной гладкой кривой. В этом случае континуальные уравнения можно получить разложением в ряд Тейлора. Такой подход получил название однополевой модели, который совпадает с классическим микрополярным описанием. В случае высокочастотных колебаний зависимость перемещений от времени является быстро меняющейся функцией, поэтому нельзя провести стандартную процедуру разложения в ряд. Однако если разделить все частицы на чётные и нечётные и рассматривать колебания этих групп отдельно, то для каждой из них станет возможным разложение в ряд. При исследовании движения частиц в решётках подразумевается, что атомы можно считать материальными точками, соединёнными между собой линейными пружинами.
Однополевая модель[править]
Изучается квадратная решётка с периодом а. Рассматривается взаимодействие центральной частицы (m,n) c четырьмя соседними частицами: (m+1,n);(m-1,n);(m,n+1);(m,n-1) в случае неустойчивой решётки, и с 8-ю - в случае устойчивой. Взаимодействие между частицами с одинаковыми массами m моделируется посредством пружин жесткостью С. Рассмотрим распространение плоской волны , полагая y_m = 0.
Неустойчивая решётка[править]
- Дискретное уравнение движения:
- Разложение в ряд Тейлора смещений частиц, соседних центральной:
- Континуальное уравнение:
- Получившееся решение:
Устойчивая решётка[править]
Двухполевая модель[править]
Неустойчивая решётка[править]
- Дискретные уравнение движения:
- Континуальные уравнение после замены переменных на акустическую и оптическую:
- Получившееся решение (решение для u аналогично решению уравнения однополевой модели):
Устойчивая решётка[править]
Выводы[править]
B результате проведённых исследований были получены уравнения распространения плоских волн в материалах, чья структура описывается моделью квадратной кристаллической решётки. Были рассмотрены два типа квадратных решёток, для каждой построены многополевые модели, в которых показано, что они применимы для моделирования длинноволновых эффектов, т.к. содержат в себе однополевую (классическую) модель, и при этом уточняют её при рассмотрении коротковолновых эффектов.
Четырёхполевая модель объединяет уравнения классической однополевой модели и уравнения двухполевых моделей, построенные с разными методами выделения подрешёток, и может быть использована для описания разных типов волн, как коротких, так и длинных. Сравнение результатов, полученных для устойчивой и неустойчивой решёток показало, что качественных различий в уравнениях не наблюдается.
Основные планируемые результаты[править]
Планируется переход к более сложным решёткам (с разными типами частиц, с пружинами разной жёсткости, etc), а также получение численных результатов для четырёхполевых моделей для обеих типов решёток.