Цилиндр внутри полого цилиндра — различия между версиями
(→Решение) |
(→Решение) |
||
| Строка 30: | Строка 30: | ||
<math> \ddot \varphi - \frac{R}{3(R-r)} \ddot \psi + \frac{2g}{3(R-r)} \sin(\varphi) = 0 </math> | <math> \ddot \varphi - \frac{R}{3(R-r)} \ddot \psi + \frac{2g}{3(R-r)} \sin(\varphi) = 0 </math> | ||
| − | + | При малых <math> \varphi </math> второе уравнение можно записать так: | |
| + | |||
| + | <math> \ddot \varphi - \frac{R}{3(R-r)} \ddot \psi + \frac{2g}{3(R-r)}\varphi = 0 </math> | ||
== Программа == | == Программа == | ||
Текущая версия на 12:34, 27 июня 2015
Проектная деятельность по информатике > Курсовые проекты Группы 09 2015 > Цилиндр внутри полого цилиндраКурсовой проект по информатике
Исполнитель: Александр Смирнов
Группа: 09 (23604)
Семестр: весна 2015
Условие задачи[править]
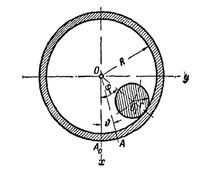
Шероховатый цилиндр массы m и радиуса r катится без скольжения по внутренней поверхности полого цилиндра массы M и радиуса R, могущего вращаться около своей горизонтально расположенной оси O. Моменты инерции цилиндров относительно своих осей равны mr2/2 и MR2. Составить уравнения движения системы и найти их первые интегралы.
Решение[править]
где - функция Лагранжа
- кинетическая энергия системы, - потенциальная энергия системы
Выбрав обобщенные координаты и получим:
При малых второе уравнение можно записать так:
Программа[править]
Программа написана на JavaScript с использованием следующих библиотек: Zepto (DOM-навигация), Three.js (WebGL-отрисовка), Dat-gui.js (интерфейс).