Распределение тепла в одномерном кристалле — различия между версиями

Версия 13:03, 14 июня 2015 (править) Денис (обсуждение | вклад) (→‎Задание начальных перемещений) ← Предыдущая правка		Версия 13:03, 14 июня 2015 (править) (отменить) Денис (обсуждение | вклад) (→‎top) Следующая правка →
Строка 2:		Строка 2:
	Научный руководитель: [[Антон_Кривцов|Кривцов А. М.]]		Научный руководитель: [[Антон_Кривцов|Кривцов А. М.]]
−
−	Презентация: [[media: Presentation7.ppt|Моделирование динамики толпы]]
	== Введение ==		== Введение ==

---

Версия 13:03, 14 июня 2015

Выполнил: Цветков Д. В.

Научный руководитель: Кривцов А. М.

Введение

На данный момент одной из наиболее активно развивающихся областей современной механики является механика наноструктур. Благодаря нанотехнологиям появляется возможность получать практически идеальные, бездефектные материалы. Требуется уметь предугадывать свойства и поведение таких материалов. Благодаря развитию компьютерных технологий имеется возможность моделировать достаточно крупные фрагменты материала, и исследовать их поведение на требуемом отрезке времени.

Также важной темой является исследование Парадокса возврата, следующего из теоремы Пуанкаре о возвращении, по отношению к достаточно коротким одномерным кристаллам. Суть Парадокса возврата в противоречии между возможностью молекул вещества любой динамической системы, сохраняющей механическую энергию, вернуться в окрестность своего первоначального положения, и такими необратимыми процессами, как теплопроводность или диффузия.

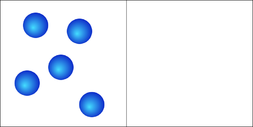
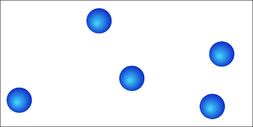
Пример: сосуд, разделенный перегородкой (рис.1а). В левой части сосуда содержится небольшое количество молекул газа, правая часть сосуда пуста. Убираем перегородку (рис.1б). Постепенно молекулы газа занимают все пространство сосуда (рис.1в). Но, так как молекул очень мало, через некоторое время они снова одновременно окажутся в левой части сосуда (рис.1г).

• Сосуд с небольшим количеством молекул газа
• 

  Рис.1а)

• 

  Рис.1б)

• 

  Рис.1в)

• 

  Рис.1г)

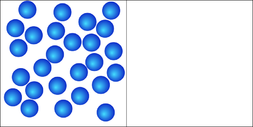
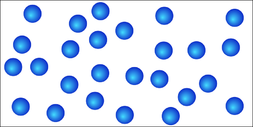
Если в начальный момент времени в левой части сосуда будет больше молекул (рис.2а), то, после удаления перегородки (рис.2б) ждать возвращения системы в начальное состояние (когда все молекулы находятся в левой части сосуда) придется намного дольше. В этом и состоит разгадка Парадокса возврата --- для достаточно большого тела вероятность обращения таких процессов, как теплопроводность, настолько мала, что время на ожидание такого возврата много больше времени существования вселенной.

• Сосуд с большим количеством молекул газа
• 

  Рис.2а)

• 

  Рис.2б)

Важно исследовать граничное время, в которое возврат системы становится практически невозможен.

В этой связи в данной работе рассматривается процесс преобразования механической энергии нелинейного одномерного стержня в тепловую и обратно с течением времени. Исследуется влияние флуктуаций скоростей на скорость преобразования энергии.

Сравнительный анализ решений задач теплопроводности для бесконечного слоя, находящегося под воздействием ультракороткого лазерного импульса

Метод исследования

Рассматривается задача одномерного теплоизолированного кристалла, нагретого ультракоротким лазерным импульсом. Производится сравнение следующих решений:

• стохастическое решение --- задача динамики кристалла, температура кристалла задается с помощью случайных скоростей
• численное решение дифференциального уравнения, полученного в ^[1]:

[math] \ddot T + \frac 1t \dot T = c^2 T'' [/math]

• аналитическое решение, полученное в ^[2]:

[math] T(t, x) = \frac1\pi \int\limits_{-t}^t \frac{e^{-\gamma \left|x - ct \right| }I_0}{k\sqrt{t^2 - \tau^2}} \,d\tau, [/math]

где [math]I_0[/math] --- интенсивность входящего пучка света, [math]\gamma[/math] --- коэффициент поглощения света.

Для численного расчета и сравнения задач написано специальное программное обеспечение на языке MATLAB.

Постановка стохастической задачи

Рассмотрим одномерный кристалл: цепочку одинаковых частиц массы [math]m[/math], соединенных одинаковыми линейными пружинами с жесткостью [math]C[/math]:

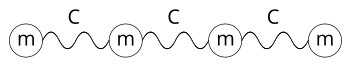
Уравнения динамики кристалла имеют вид:

[math] \ddot u_n = \omega_0^2 (u_{n-1} - 2u_n + u_{n+1}),\quad \omega_0 = \sqrt{\frac{C}{m}}, [/math]

где [math]u_n[/math] --- перемещение [math]n[/math]-й частицы; [math]n[/math] --- индекс, принимающий произвольные целые значения, [math]C[/math] --- жесткость связи между частицами, [math]m[/math] --- масса частицы.

Температура в кристалле определяется как дисперсия скоростей частиц. Скорости частиц задаются с помощью генератора случайных чисел.

Начальные условия

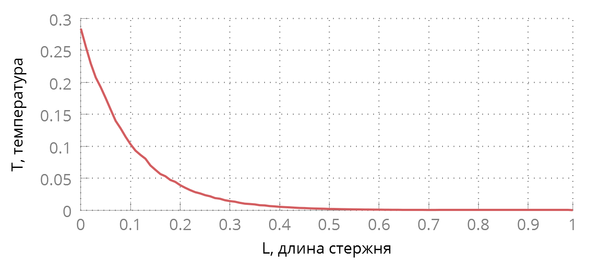
Требуемое распределение температуры по координате в кристалле на начальный момент времени описывается формулой:

[math] T_0(x) = \frac{I_0}k e^{-\gamma x} [/math]

где [math]I_0[/math] --- интенсивность входящего пучка света, [math]\gamma[/math] --- коэффициент поглощения света, [math]k[/math] --- постоянная Больцмана. Согласно закону Бугера ^[3], данные начальные условия можно интерпретировать как результат воздействия на кристалл ультракороткого лазерного импульса.

Задание начальных скоростей

Температура в кристалле задается с помощью скоростей. Воспользуемся определением кинетической температуры для одномерного случая:

[math] kT(x) = m\overline{v_x^2}, [/math]

где [math]k[/math] --- постоянная Больцмана, [math]\overline x = f(x)[/math] --- оператор усреднения по координате. Выразим [math]\overline{v_x^2}[/math]:

[math] \overline{v_x^2} = \frac{kT(x)}m [/math]

Для того, чтобы получить требуемое распределение, будем задавать скорости с помощью случайного числа [math]\rho[/math] в диапазоне [math][-1; 1][/math].

Посчитаем, чему равно [math]\overline{\rho^2}[/math]:

[math] \overline{\rho^2} = \frac 1 2 \int\limits_a^b \rho^2 \,d\rho = \frac 1 2 \left. \frac {\rho^3}3 \right|_{-1}^1 = \frac 1 3 [/math]

Значит [math]3\overline{\rho^2} = 1[/math].

Заменим [math]T(x)[/math] на [math]T_0(x)[/math], генерируемое с помощью [math]\overline{\rho^2}[/math]:

[math] \overline{v_x^2} = \frac{3k\overline{\rho^2}T_0(x)}m [/math]

Выразим [math]v_x[/math]:

[math] v_x^2 = 3\rho^2 T_0(x) [/math]

[math] v_x = \rho\sqrt{3T_0(x)} [/math]

При генерации скорости с помощью данной формулы, получается требуемое распределение температуры по координате:

Задание начальных перемещений

Если задать нулевые начальные перемещения, то потенциальная энергия кристалла будет равна нулю, и с течением времени примерно половина кинетической энергии преобразуется в потенциальную ^[1]. Чтобы этого избежать, начальные перемещения задаются с помощью деформаций. Деформации задаются таким образом, чтобы кинетическая и потенциальная энергии кристалла в начальный момент времени были равны.

Сначала задаются [math]N-1[/math] случайных чисел, сумма которых равна нулю:

[math] \sum_{i=0}^{N-1}{\rho_i} = 0, [/math]

где [math]N[/math] --- количество частиц в цепочке. После рассчитывается параметр [math]\varPi_{\rho}[/math]:

[math] \varPi_{\rho} = C\sum_{i=0}^{N-1}{\rho^2_i} [/math]

и кинетическая энергия [math]K[/math]:

[math] K = m\sum_{i=0}^{N}{v^2_i} [/math]

Далее, с помощью отношения [math]K[/math] к [math]\varPi_{\rho}[/math] находятся деформации:

[math] \varepsilon_i = \rho_i\sqrt{\frac K\varPi_{\rho}} [/math]

Результаты

Задача о переходе энергии механических колебаний в тепло для нелинейного одномерного кристалла

Постановка задачи

Детерминированная задача

Начальные условия

Метод определения формы кристалла в различные моменты времени

Анализ решения задачи на большом отрезке времени

Зависимость времени возвращения кристалла к начальному состоянию от количества частиц и амплитуды синуса

Высота второго пика

Стохастическая задача

Начальные условия

Время перехода механической энергии в тепловую

Заключение

1. ↑ ^{1,0 1,1} Ошибка цитирования Неверный тег <ref>; для сносок krivtsov_1dcrystal_2014 не указан текст
2. ↑ Ошибка цитирования Неверный тег <ref>; для сносок babenkov_tcvetkov не указан текст
3. ↑ Ошибка цитирования Неверный тег <ref>; для сносок Putilov1963 не указан текст