КП: Эффект Магнуса — различия между версиями

Версия 13:20, 12 мая 2015

Курсовой проект по Теоретической механике

Исполнитель: Шварёв Николай

Группа: 09 (23604)

Семестр: весна 2015

Сила Магнуса

Аннотация проекта

Формулировка задачи

Построение и исследование математической модели движения объекта (в нашем случае футбольного мяча), получение уравнения его движения и построение траектории в трехмерном пространстве с учётом различных внешних факторов, влияющих на движение, таких как сила сопротивления воздуха и эффект Магнуса.

Общие сведения по теме

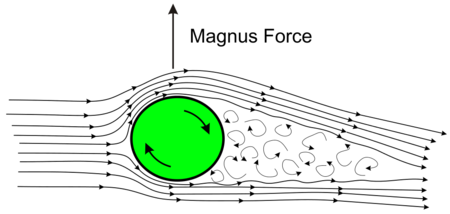
Эффект Магнуса - образование подъемной силы, действующей на вращающееся тело при обтекании его потоком жидкости или газа.

Пример влияния силы Магнуса на траекторию движения мяча

Решение

Силу сопротивления воздуха будем считать с помощью закона Стокса:

[math]\vec{F} = -6πrη\vec{v} [/math] , где

[math]\vec{F}[/math] - сила Стокса,

[math]r[/math] - радиус мяча,

[math]η[/math] - динамическая вязкость,

[math]\vec{v}[/math] - скорость мяча.

Силу Магнуса примем вида:

[math]\vec{F} = 8πρr^3\vec{u}\times\vec{ω} [/math] , где

[math]\vec{F}[/math] - сила Магнуса,

[math]ρ[/math] - плотность воздуха,

[math]r[/math] - радиус мяча,

[math]\vec{u}[/math] - относительная скорость мяча,

[math]\vec{ω}[/math] - угловая скорость мяча.

Применив метод Эйлера, получим формулы для нахождения скорости и координаты мяча:

[math] \begin{cases} v_x^{i+1} = v_x^i + (-6πrηv_x^i/m + 8πρr^3(u_y^iω_z - u_z^iω_y)/m)\Delta t \\ v_y^{i+1} = v_y^i + (-6πrηv_y^i/m + 8πρr^3(u_z^iω_w - u_x^iω_z)/m)\Delta t \\ v_z^{i+1} = v_z^i + (-6πrηv_z^i/m + 8πρr^3(u_x^iω_y - u_y^iω_x)/m)\Delta t \\ \end{cases} [/math]

[math] \begin{cases} x^{i+1} = x^i + v_x^i\Delta t \\ y^{i+1} = y^i + v_y^i\Delta t \\ z^{i+1} = z^i + v_z^i\Delta t \\ \end{cases} [/math];

Обсуждение результатов и выводы

Скачать отчет:
Скачать презентацию:

Ссылки по теме

См. также

• Справочная информация
• Курсовые проекты ТМ