Определимые связи — различия между версиями
Hofa (обсуждение | вклад) |
Hofa (обсуждение | вклад) |
||
| (не показано 26 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | + | Дискуссия между '''Ф.Ф.Прохоренко (ФП)''' и '''А.В.Костаревым (АК)''' | |
| − | |||
| − | |||
| + | '''ФП''': Хотелось бы знать, как как могут помочь магические заклинания об избыточности или недостаточности связей в каких-то (в каких ?) направлениях. | ||
<div style="float:right"> | <div style="float:right"> | ||
| Строка 8: | Строка 7: | ||
</div> | </div> | ||
| − | + | '''АВ''':Студентам я привожу такой пример. | |
| − | + | Пусть требуется закрепить тело связями, совместимыми с произвольной нагрузкой.Глухая заделка конечно подойдет, но консольное закрепление тела вызовет большие реакции в заделке. | |
| − | :Студентам я привожу такой пример. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Поставим в произвольной точка А тела сферический шарнир. Если в другой точке В поставить второй сферический шарнир, то число неизвестных станет равным шести, и может показаться, что задача окажется cтатически определимой. Однако это не так. | ||
| + | При установке двух сферических шарниров, появляется избыточность связей вдоль соединяющей их линии, поскольку реакции шарниров могут оказаться на одной линии (шарниры второй раз фиксируют расстояние между точками). | ||
| + | |||
| + | В то же время указанные шарниры недостаточны для произвольной пространственной нагрузки, поскольку возможен поворот тела вокруг оси, проходящей через шарниры. | ||
| + | Избыточность связей исчезнет, если вместо второго сферического шарнира поставить цилиндрический шарнир. Ось цилиндрического шарнира не может быть перпендикулярна линии АВ, иначе опять возникнет избыточность связей вдоль линии шарниров. | ||
| + | |||
| + | Реакции в шарнирах будут стремиться к бесконечности при стремлении угла между осью шарнира и линией АВ к 90о. '''Разве это не опасно?''' | ||
Теперь число неизвестных станет равным пяти, но несовместимость связей с произвольной | Теперь число неизвестных станет равным пяти, но несовместимость связей с произвольной | ||
нагрузкой сохранится. Чтобы окончательно закрепить тело, поставим в точке С еще одну связь. | нагрузкой сохранится. Чтобы окончательно закрепить тело, поставим в точке С еще одну связь. | ||
Ясно, что она должна создать лишь одну неизвестную, иначе число неизвестных станет больше шести. | Ясно, что она должна создать лишь одну неизвестную, иначе число неизвестных станет больше шести. | ||
| − | Такой связью может быть стержень на двух шарнирах. Стержень нельзя располагать в плоскости | + | Такой связью может быть стержень на двух шарнирах. Стержень нельзя располагать в плоскости АВС, иначе он будет избыточным и, одновременно, несовместным с произвольной нагрузкой. Реакции в стержне будут стремиться к бесконечности, если стержень будет приближаться к плоскости АВС. '''Разве это не опасно?''' |
| − | АВС, иначе он будет избыточным и, одновременно, несовместным с произвольной нагрузкой. | + | |
| − | Реакции в стержне будут стремиться к бесконечности, если стержень будет приближаться к | + | Чтобы реакции были минимальны при данной нагрузке, инженер выберет удаленные друг от друга точки опоры на поверхности тела, направит ось цилиндрического шарнира по АВ, а стержень перпендикулярно АВС. '''Разве это не важно понимать инженеру?''' |
| − | плоскости АВС. Разве это не опасно? | ||
| − | + | [[Файл:Body2.png|right|300px]] | |
| − | + | '''ФП''': С одним телом понятно. А вот с двумя Вы опять, по-моему, ошибаетесь: левая задача статически неопределена, а правая определена. В том можно убедиться, написав уравнения моментов вокруг шарниров обоих тел и сложив эти уравнения - моменты силы и собственно момент в скользящей заделке в задаче А)сократятся и при произвольной нагрузке система станет несовместной. | |
| − | + | Собственно говоря, я веду вас к тому, что я и написал в своих лекциях: судить об определенности. | |
| − | ''' | + | в общем случае следует по решению уравнений, потому что кинематический анализ может оказаться не более простым, чем составление уравнений равновесия. |
| + | |||
| + | '''АВ''': Инженер должен конструировать, а не решать только готовые задачи. Нарисовав любую схему связей для любой системы тел, можно составить матрицу левой части, и в Интернете найти ее определитель. Студент должен это уметь. | ||
| + | '''ФП''': Если даже мы не можем иногда дать правильный ответ « на глаз», то чего можно требовать от студентов? | ||
| − | + | '''АВ''': Инженер должен уметь оценить и на глаз в простых случаях. Это полезно и красиво. Стимулирует. В классе мы вместе со студентами изобретаем задачу на статику в пространстве. И студенты рассуждают как можно или нельзя поставить следующую связь | |
| + | |||
| + | '''ФА''': Следует ли перегружать их довольно туманными терминами «недостаточность» и «избыточность»? | ||
| + | |||
| + | '''АК''': Они просты и понятны: Достаточны связи, которые держат любую нагрузку. Избыточные повторяют связи в теле, потому и избыточные. | ||
| + | |||
| + | '''ФП''': В рассматриваемых задачах можно, конечно, провести и кинематический анализ, основанный на следующем утверждении: если конструкция допускает мгновенные скорости (т.е. кинематически изменяемая), то она статически неопределима (думаю, что в этом мы едины). | ||
| + | |||
| + | '''АВ''': Да. Хороши оба подхода, поскольку, как было сказано, при правильном числе неизвестных избыточность сопровождается недостаточностью. | ||
| − | + | На плоскости все системы тел фактически сводятся только к 2м стержням, соединенным не глухой | |
| + | заделкой 2(n+1)=3n n=2. А для двух стержней простое правило: реакции в 3х связях не должны оказаться на одной прямой. | ||
| − | + | В Вашем примере А, реакции в скользящей заделке (сила, параллельная линии шарниров и | |
| + | момент) могут привестись к одной силе на линии шарниров, поскольку скользящая заделка | ||
| + | перпендикулярна линии шарниров АВ. В этом случае три реакции могут оказаться на одной линии. Связи становятся избыточными по линии АВ и недостаточными для вращения стержней (их угловые скорости одинаковы, независимо от длин и углов). | ||
| − | + | Случай В определим, поскольку заделка не перпендикулярна линии шарниров. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == См. также== | |
| − | + | [[Работы Костарева А.В]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Текущая версия на 21:58, 8 декабря 2014
Дискуссия между Ф.Ф.Прохоренко (ФП) и А.В.Костаревым (АК)
ФП: Хотелось бы знать, как как могут помочь магические заклинания об избыточности или недостаточности связей в каких-то (в каких ?) направлениях.
АВ:Студентам я привожу такой пример. Пусть требуется закрепить тело связями, совместимыми с произвольной нагрузкой.Глухая заделка конечно подойдет, но консольное закрепление тела вызовет большие реакции в заделке.
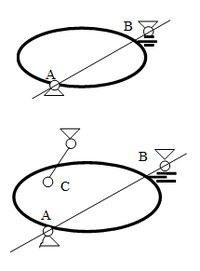
Поставим в произвольной точка А тела сферический шарнир. Если в другой точке В поставить второй сферический шарнир, то число неизвестных станет равным шести, и может показаться, что задача окажется cтатически определимой. Однако это не так. При установке двух сферических шарниров, появляется избыточность связей вдоль соединяющей их линии, поскольку реакции шарниров могут оказаться на одной линии (шарниры второй раз фиксируют расстояние между точками).
В то же время указанные шарниры недостаточны для произвольной пространственной нагрузки, поскольку возможен поворот тела вокруг оси, проходящей через шарниры. Избыточность связей исчезнет, если вместо второго сферического шарнира поставить цилиндрический шарнир. Ось цилиндрического шарнира не может быть перпендикулярна линии АВ, иначе опять возникнет избыточность связей вдоль линии шарниров.
Реакции в шарнирах будут стремиться к бесконечности при стремлении угла между осью шарнира и линией АВ к 90о. Разве это не опасно? Теперь число неизвестных станет равным пяти, но несовместимость связей с произвольной нагрузкой сохранится. Чтобы окончательно закрепить тело, поставим в точке С еще одну связь. Ясно, что она должна создать лишь одну неизвестную, иначе число неизвестных станет больше шести.
Такой связью может быть стержень на двух шарнирах. Стержень нельзя располагать в плоскости АВС, иначе он будет избыточным и, одновременно, несовместным с произвольной нагрузкой. Реакции в стержне будут стремиться к бесконечности, если стержень будет приближаться к плоскости АВС. Разве это не опасно?
Чтобы реакции были минимальны при данной нагрузке, инженер выберет удаленные друг от друга точки опоры на поверхности тела, направит ось цилиндрического шарнира по АВ, а стержень перпендикулярно АВС. Разве это не важно понимать инженеру?
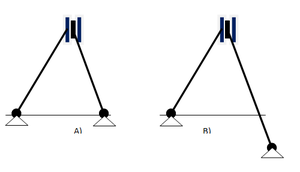
ФП: С одним телом понятно. А вот с двумя Вы опять, по-моему, ошибаетесь: левая задача статически неопределена, а правая определена. В том можно убедиться, написав уравнения моментов вокруг шарниров обоих тел и сложив эти уравнения - моменты силы и собственно момент в скользящей заделке в задаче А)сократятся и при произвольной нагрузке система станет несовместной. Собственно говоря, я веду вас к тому, что я и написал в своих лекциях: судить об определенности. в общем случае следует по решению уравнений, потому что кинематический анализ может оказаться не более простым, чем составление уравнений равновесия.
АВ: Инженер должен конструировать, а не решать только готовые задачи. Нарисовав любую схему связей для любой системы тел, можно составить матрицу левой части, и в Интернете найти ее определитель. Студент должен это уметь.
ФП: Если даже мы не можем иногда дать правильный ответ « на глаз», то чего можно требовать от студентов?
АВ: Инженер должен уметь оценить и на глаз в простых случаях. Это полезно и красиво. Стимулирует. В классе мы вместе со студентами изобретаем задачу на статику в пространстве. И студенты рассуждают как можно или нельзя поставить следующую связь
ФА: Следует ли перегружать их довольно туманными терминами «недостаточность» и «избыточность»?
АК: Они просты и понятны: Достаточны связи, которые держат любую нагрузку. Избыточные повторяют связи в теле, потому и избыточные.
ФП: В рассматриваемых задачах можно, конечно, провести и кинематический анализ, основанный на следующем утверждении: если конструкция допускает мгновенные скорости (т.е. кинематически изменяемая), то она статически неопределима (думаю, что в этом мы едины).
АВ: Да. Хороши оба подхода, поскольку, как было сказано, при правильном числе неизвестных избыточность сопровождается недостаточностью.
На плоскости все системы тел фактически сводятся только к 2м стержням, соединенным не глухой заделкой 2(n+1)=3n n=2. А для двух стержней простое правило: реакции в 3х связях не должны оказаться на одной прямой.
В Вашем примере А, реакции в скользящей заделке (сила, параллельная линии шарниров и момент) могут привестись к одной силе на линии шарниров, поскольку скользящая заделка перпендикулярна линии шарниров АВ. В этом случае три реакции могут оказаться на одной линии. Связи становятся избыточными по линии АВ и недостаточными для вращения стержней (их угловые скорости одинаковы, независимо от длин и углов).
Случай В определим, поскольку заделка не перпендикулярна линии шарниров.