Тепловое расширение кристаллов (компьютерное моделирование) — различия между версиями
м (переименовал Тепловое расширение кристаллов в Тепловое расширение кристаллов (компьютерное моделирование)) |
|||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 15: | Строка 15: | ||
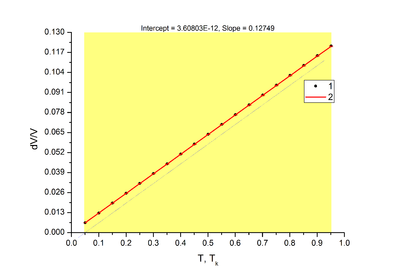
[[Файл:Graph2.png|400px|thumb|left|Рис. 1. Зависимость объёмной деформации от температуры. 1 - Значение определённое при усреденении по всему интервалу, 2 - усреднение по малым интервалам]] | [[Файл:Graph2.png|400px|thumb|left|Рис. 1. Зависимость объёмной деформации от температуры. 1 - Значение определённое при усреденении по всему интервалу, 2 - усреднение по малым интервалам]] | ||
| + | |||
| + | <br style="clear: both" /> | ||
== См. также == | == См. также == | ||
* [[Корреляции перемещений в кристаллах (компьютерное моделирование)]] | * [[Корреляции перемещений в кристаллах (компьютерное моделирование)]] | ||
Текущая версия на 14:38, 27 июля 2014
Расчеты: Панченко Артём
Для определения коэффициента теплового расширения использовалось два подхода: при постоянном объёме и постоянном давлении (с помощью баростата давление приближалось к нулю).
ГЦК решетка[править]
Потенциал Леннард-Джонса[править]
Постоянный объём[править]
ГЦК кристалл 30x30x30 ГЦК ячеек (??? частиц), периодические граничные условия, релаксация системы в течении 10*Tp, Tp = T0p/200, полное время определения давления 20*Tp, время определения точек среднего 3*Tp. Температура системы от 1e-7*Tk, до 1.9e-6*Tk. На первом шаге задаются начальные скорости согласно нормальному распределению, затем система релаксирует, и далее вычисляется давление на основе метода Кривцова-Кузькина.
Коэффициент теплового расширения определённый по первой точке: 0.127474, теоретическое значение: 0.131944, относительно отклонение от теоретического значения: 3.39%.
Коэффициент теплового расширения определённый по наклону (Рис.1): 0.12749, теоретическое значение: 0.131944, относительно отклонение от теоретического значения: 3.38%.