КП: Кинематика кривошипно-шатунного механизма — различия между версиями

Версия 16:00, 30 мая 2014

Курсовой проект по Теоретической механике

Исполнитель: Cолодовников Владислав

Группа: 08 (23604)

Семестр: весна 2014

Аннотация проекта

Данный проект посвящен Кинематическому анализу движения кривошипно-шатунного механизма в двигателе внутреннего сгорания. Кривошипно-шатунный механизм (КШМ) предназначен для преобразования возвратно-поступательного движения поршня во вращательное движение (например, во вращательное движение коленчатого вала в двигателях внутреннего сгорания), и наоборот.

Постановка задачи

• Установление законов движения поршня и шатуна
• Составить уравнения перемещения, ускорения и скорости поршня и шатуна

Постановка задачи

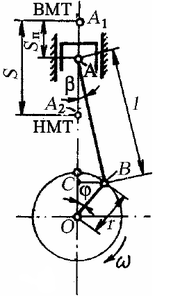
Дан центральный кривошипно-шатунный механизм, у которого ось цилиндра пересекается с осью коленчатого вала.

Примем следующие обозначения:
φ — угол поворота кривошипа в рассматриваемый момент времени
При φ =0 поршень занимает крайнее положение А1 – ВМТ
При φ =180° поршень занимает положение A2 – НМТ
β – угол отклонения оси шатуна
ω= πn/30 – угловая скорость вращения кривошипа
r = OB – радиус кривошипа
L = AB — длина шатуна
λ = r/L – безразмерный параметр КШМ
S = 2r = A1A2 — полный ход поршня

Решение

Перемещение поршня:
При повороте кривошипа на угол φ перемещение поршня от его начального положения в ВМТ определяется отрезком АА1 и равно: Sп = AA1 = A1O− AO = A1O − (OC + CA) .

[math] S= R+L-(rcos\varphi+Lcos\beta )=r\left [ 1+L/R-(cos\varphi+L/Rcos\beta ) \right ]=r\left [( 1-cos\varphi ) +1/\lambda (1-cos\beta )\right ] [/math]
[math] sin\beta =r/L*sin\varphi=\lambda sin\varphi [/math]
Следовательно, [math] cos\beta =\sqrt{s1-sin^2\beta }=\sqrt{1-\lambda ^2sin^2\varphi} =(1-\lambda ^2sin^2\varphi )^{1/2} [/math]
т.к. [math] cos\beta =1-1/2*\lambda ^2sin^2\varphi, [/math]
[math] S=r\left [ (1-cos\varphi )+\lambda /2*sin^2 \varphi ] [/math]
но т.к. [math] sin^2\varphi =\frac{1-cos2\varphi }{2} [/math] , то
[math] S=r\left [ (1-cos\varphi )+\lambda /4*(1-cos2\varphi ) \right ] [/math] - это выражение описывает перемещение поргня в зависимости от угла поворота кривошипа и геометрических размеров КШМ

Скорость поршня:
Выражение для определения скорости перемещения поршня как функцию угла поворота кривошипа можно получить путем дифференцирования по времени левой и правой части уравнения движения кривошипно-шатунного механизма.
[math] \frac{\mathrm{ds} }{\mathrm{d} t }=\frac{\mathrm{d} }{\mathrm{d} \varphi }\left \{ r\left [ (1-cos\varphi )+\lambda /4(1-cos2\varphi ) \right ] \right \}\frac{\mathrm{d\varphi } }{\mathrm{d} t}=r(sin\varphi +\frac{\lambda }{2}sin2\varphi )\frac{\mathrm{d\varphi } }{\mathrm{dt}} [/math],
где [math] \frac{\mathrm{ds} }{\mathrm{d} t }=\nu [/math] - скорость перемещения поршня;[math] \frac{\mathrm{d\varphi } }{\mathrm{dt}}=\omega [/math] - угловая скорость вращения кривошипа.
Следовательно имеем:
[math] \nu =r\omega(sin\varphi+ \frac{\lambda }{2}sin2\varphi) [/math]

Ускорение поршня:
Выражение для определения ускорения поршня можно найти путем дифференцирования по времени выражения для скорости поршня:
[math] j=\frac{\mathrm{d\nu } }{\mathrm{d} t}=\frac{\mathrm{d\nu } }{\mathrm{dt}}\frac{\mathrm{d\varphi } }{\mathrm{dt}}=r\omega\frac{\mathrm{d\varphi } }{\mathrm{dt}}cos\varphi +\frac{\lambda r\omega}{2}*2\frac{\mathrm{d\varphi } }{\mathrm{dt}}cos2\varphi [/math] ,
откуда [math] J=r\omega^2cos\varphi+\lambda r \omega^2cos2\varphi=r \omega^2(cos\varphi+\lambda cos2\varphi) [/math]

Кинематика шатуна:

При вращении кривошипа шатун совершает сложное плоскопараллельное движение, которое можно рассматривать как сумму поступательного движения вместе с поршнем (с точкой А на рис. 9), кинематика которого рассмотрена, и углового движения относительно оси поршневого пальца, т. е. точки А.
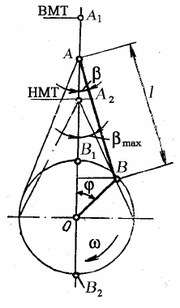
Угловое перемещение шатуна шатуна относительно оси цилиндра определяется из уравнения:
[math] sin\beta =r/L*sin\varphi=\lambda sin\varphi [/math] (*):
[math]\beta =arcsin(\lambda sin\varphi)[/math]
Из последнего уравнения видно, что наибольшее отклонение шатуна при [math] \varphi=\pi /2 [/math] и [math] \varphi=3\pi/2 [/math],что соответствует [math] \beta_{max}=\pm arcsin \lambda..[/math]
Продифференцировав выражение (*) как уравнение с разделенными переменными, имеем

Угловая скорость шатуна ωш определяется путем дифференцирования по времени функции углового перемещения:
[math] \omega=\frac{\mathrm{d\beta} }{\mathrm{d} t}=\frac{\mathrm{d\beta} }{\mathrm{d} \varphi}\frac{\mathrm{d\varphi} }{\mathrm{d} t}=\omega\frac{\mathrm{d\beta} }{\mathrm{d} t} [/math]
Продифференцировав выражение (*) как уравнение с разделенными переменными, имеем [math] cos\beta d\beta=\lambda cos\varphi d \varphi [/math],
откуда [math] \frac{d\beta}{d\varphi}=\lambda\frac{cos \varphi}{cos \beta } [/math]
[math] \omega = \omega \lambda\frac{cos \varphi}{cos \beta } = \frac{\omega \lambda cos \varphi}{\sqrt{1-\lambda^2 sin^2 \varphi}}\approx \omega \lambda cos \varphi [/math]

Угловое ускорение шатуна определяется путем дифференцирования по времени функции угловой скорости его:
[math] \varepsilon =\frac{\mathrm{d\omega} }{\mathrm{d} t}=\frac{\mathrm{d\omega} }{\mathrm{d} \varphi}*\frac{\mathrm{d\varphi} }{\mathrm{d} t}=-\frac{\omega^2\lambda (1-\lambda^2)}{1-\lambda^2sin^2\varphi)^{3/2}}sin\varphi\approx -\omega^2\lambda sin\varphi [/math]