КП: Корпоративный чат — различия между версиями

Версия 22:39, 22 мая 2014 (править) Paul (обсуждение | вклад) ← Предыдущая правка		Версия 22:41, 22 мая 2014 (править) (отменить) Paul (обсуждение | вклад) Следующая правка →
Строка 27:		Строка 27:
	<math>m \ddot{u} = C \ (u_{n+1} - 2 \ u_n + u_{n-1}) </math> <br>		<math>m \ddot{u} = C \ (u_{n+1} - 2 \ u_n + u_{n-1}) </math> <br>
	<math>w_0 = \sqrt{C / m} </math> <br>		<math>w_0 = \sqrt{C / m} </math> <br>
		+	<math>m \ddot{u} = w_0^2 \ (u_{n+1} - 2 \ u_n + u_{n-1}) </math> <br>
−	где Cx и Cy - жесткости пружин, m - масса грузика, B - вязкость среды <br>
−	Складываемые колебания имеют вид:<br>
−	<math> x = A_x \cos (\omega_xt+\alpha_x) </math><br>
−	<math> y = A_y \cos (\omega_yt+\alpha_y) </math><br>
−	Частоты колебаний определяются как <math>\omega_x = \sqrt{\frac{C_x}{m}},\omega_y = \sqrt{\frac{C_y}{m}}</math><br>
−	[[Файл:Liss.jpg|300px]]
	== Результат ==		== Результат ==

---

Версия 22:41, 22 мая 2014

А.М. Кривцов > Теоретическая механика > Курсовые проекты 2014 > Моделирование колебаний (пружина + груз) (JS)

---

Курсовой проект по Теоретической механике

Исполнитель: Киселев Павел

Группа: 08 (23604)

Семестр: весна 2014

Аннотация проекта

Проект направлен на изучение колебания тела на пружине и моделирование этого процесса на языке JavaScript

Постановка задачи

- Изучить колебания тела на пружине

- Написать программу, моделирующую колебания системы из n тел и (n+1) пружин в горизонтальной плоскости

Общие сведения по теме

Закон Гука — уравнение теории упругости, связывающее напряжение и деформацию упругой среды.
Для тонкого растяжимого стержня закон Гука имеет вид:
[math] F = k \ Delta\ (l) [/math]
Рассмотрим систему тел:
[math] m \ddot{u} = F_{n+1} - F_n [/math] (1)( 2-й закон Ньютона )
[math]F_{n+1} = C \ (u_{n+1} - u_n) [/math] ; [math]F_n = C \ (u_n - u_{n-1}) [/math]
Подставим в (1):
[math]m \ddot{u} = C \ (u_{n+1} - 2 \ u_n + u_{n-1}) [/math]
[math]w_0 = \sqrt{C / m} [/math]
[math]m \ddot{u} = w_0^2 \ (u_{n+1} - 2 \ u_n + u_{n-1}) [/math]

Результат

Результатом работы стала программа, написанная на языке JavaScript. Возможности программы:
- Выбор простого либо сложного движения( под простым движением подразумевается учитывание только силы упругости вдоль оси, в сложном же - учитывается и сила упругости, и сила деформации пружины действующая под углом)
- Возможность изменения массы, жесткости пружин по оси абцисс и ординат, вязкость среды
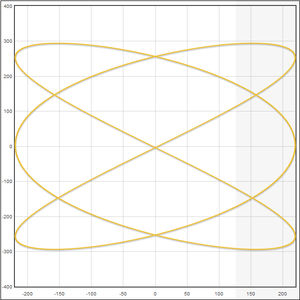
- Визуальное отображение траектории движения грузика с возможностью очистки графика
Моделирование фигур Лиссажу методом пружин

Ссылки по теме

Моделирование фигур Лиссажу методом пружин
Фигуры Лиссажу

См. также

• Справочная информация
• Курсовые проекты 2013
• Курсовые проекты 2012
• JavaScript-программирование