Кристаллическая решетка алмаза — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(→Безразмерные параметры координационного тензора) |
|||
| (не показано 6 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | [[ | + | [[ТМ|Кафедра ТМ]] > [[Научный справочник]] > [[Кристаллические решетки]] > '''Решетка алмаза''' <HR> |
| − | [[Файл: diamond.gif|thumb|]] | + | |
| + | [[File:R5.gif|250px|thumb]] | ||
| + | |||
| + | <!--[[Файл: diamond.gif|thumb|]]--> | ||
| + | |||
| + | == Структура решетки == | ||
| + | |||
| + | |||
| + | [[Файл: 58.jpg|thumb|]] | ||
| + | |||
| + | Эта решетка может быть получена из [[ОЦК]] удалением с первой координационной сферы каждого второго атома так, чтобы оставшиеся атомы лежали на вершинах тетраэдра. Решетка алмаза сложная, состоит из двух простых подрешеток. Область пространства, лежащая ближе к данному атому, чем к остальным атомам,<REF>Для сложных решеток подобную область называют [https://ru.wikipedia.org/wiki/%D0%94%D0%B8%D0%B0%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B0_%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D0%BE%D0%B3%D0%BE многогранником Вороного].</REF> для решетки алмаза представляет собой [https://en.wikipedia.org/wiki/Triakis_truncated_tetrahedron Триакисов усеченный тетраэдр]. | ||
| + | |||
| + | == Распространенность в природе == | ||
| + | |||
| + | Данной решеткой обладает алмаз, а также элементы четвертой группы: кремний, германий и <math>\alpha</math>-олово. | ||
| − | == | + | == Геометрия решетки == |
| − | + | Орты (единичные векторы) <math>{\bf n}_\alpha</math>, задающие направление от некоторого атома кристаллической решетки к его ближайшим соседям, могут быть представлены в виде: | |
| − | == | + | :<math> |
| + | \textbf{n}_{1}=\frac{1}{\sqrt{3}}(\textbf{i}+ \textbf{j}+\textbf{k}),\quad | ||
| + | \textbf{n}_{2}=\frac{1}{\sqrt{3}}(-\textbf{i}-\textbf{j}+\textbf{k}), | ||
| + | </math> | ||
| − | <math>\textbf{n}_{ | + | :<math> |
| + | \textbf{n}_{3}=\frac{1}{\sqrt{3}}(\textbf{i}-\textbf{j}-\textbf{k}), \quad | ||
| + | \textbf{n}_{4}=\frac{1}{\sqrt{3}}(-\textbf{i}+ \textbf{j}-\textbf{k}), | ||
</math> | </math> | ||
| − | |||
| − | |||
| − | |||
| − | + | где <math>{\bf i},\,{\bf j},\,{\bf k}</math> — орты Декартовой системы координат. | |
| − | <math> | + | |
| − | \eta=\infty | + | Безразмерные параметры координационного тензора<REF>[[А.М. Кривцов]]. Теоретическая механика. [[Упругие свойства одноатомных и двухатомных кристаллов]]: учеб. пособие. - СПб.: Изд-во Политехн. ун-та, 2009. - 126 c.</REF> |
| − | M_\kappa=-frac{8}{9} | + | |
| − | M_\mu=frac{4}{9}. | + | :<math> |
| + | \eta=\infty, \quad | ||
| + | M_\kappa=-\frac{8}{9}, \quad | ||
| + | M_\mu=\frac{4}{9}. | ||
</math> | </math> | ||
| + | |||
| + | == Примечания == | ||
| + | <references> </references> | ||
| + | |||
| + | [[Category: Кристаллические решетки]] | ||
Текущая версия на 07:39, 26 апреля 2014
Кафедра ТМ > Научный справочник > Кристаллические решетки > Решетка алмаза
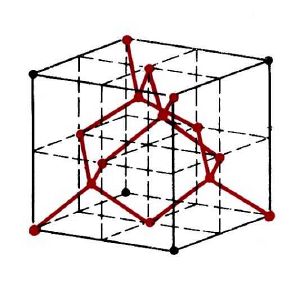
Структура решетки[править]
Эта решетка может быть получена из ОЦК удалением с первой координационной сферы каждого второго атома так, чтобы оставшиеся атомы лежали на вершинах тетраэдра. Решетка алмаза сложная, состоит из двух простых подрешеток. Область пространства, лежащая ближе к данному атому, чем к остальным атомам,[1] для решетки алмаза представляет собой Триакисов усеченный тетраэдр.
Распространенность в природе[править]
Данной решеткой обладает алмаз, а также элементы четвертой группы: кремний, германий и -олово.
Геометрия решетки[править]
Орты (единичные векторы) , задающие направление от некоторого атома кристаллической решетки к его ближайшим соседям, могут быть представлены в виде:
где — орты Декартовой системы координат.
Безразмерные параметры координационного тензора[2]
Примечания[править]
- ↑ Для сложных решеток подобную область называют многогранником Вороного.
- ↑ А.М. Кривцов. Теоретическая механика. Упругие свойства одноатомных и двухатомных кристаллов: учеб. пособие. - СПб.: Изд-во Политехн. ун-та, 2009. - 126 c.