Бразгина Ольга. Теория пластичности: проблемы и пути решения — различия между версиями
(→Феноменологические теории пластичности) |
Young1990 (обсуждение | вклад) (→Феноменологические теории пластичности) |
||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 11: | Строка 11: | ||
[[Файл: Gisteresys.png|thumb|left]] | [[Файл: Gisteresys.png|thumb|left]] | ||
[[Файл: several_tpt.png|thumb|left]] | [[Файл: several_tpt.png|thumb|left]] | ||
| − | Используется критерий Мизеса или Треска для определения момента начала пластического течения. Рассматриваются три типа законов упрочнения: изотропный, кинематический, комбинированный. | + | Используется критерий [[Рихард_фон_Мизес|Мизеса]] или Треска для определения момента начала пластического течения. Рассматриваются три типа законов упрочнения: изотропный, кинематический, комбинированный. |
Данная теория позволяет с достаточной для прикладных задач МДТТ точностью описывать процессы при близких к простым нагружениях(деформирование по траекториям малой кривизны). | Данная теория позволяет с достаточной для прикладных задач МДТТ точностью описывать процессы при близких к простым нагружениях(деформирование по траекториям малой кривизны). | ||
На данный момент теория широко используется, вводятся многоповерхностные теории и варьируются законы упрочнения. | На данный момент теория широко используется, вводятся многоповерхностные теории и варьируются законы упрочнения. | ||
| Строка 30: | Строка 30: | ||
В последнее время наиболее развивающийся класс моделей. С уровня реального тела спускаемся на уровень поликристалла, и далее вплоть до атомного уровня. Хотя в моделях этого типа максимально учитываются физические аспекты, на нижнем уровне необходимо зхамыкать модеть феноменологическими уравнениями, что также приводит к сложностям. Более того, возникают проблемы, связанные с вычислительной погрешностью и погрешностью согласования уровней. | В последнее время наиболее развивающийся класс моделей. С уровня реального тела спускаемся на уровень поликристалла, и далее вплоть до атомного уровня. Хотя в моделях этого типа максимально учитываются физические аспекты, на нижнем уровне необходимо зхамыкать модеть феноменологическими уравнениями, что также приводит к сложностям. Более того, возникают проблемы, связанные с вычислительной погрешностью и погрешностью согласования уровней. | ||
[[Файл: two-level.bmp|thumb|left]] | [[Файл: two-level.bmp|thumb|left]] | ||
| + | |||
| + | [[Category: Студенческие проекты]] | ||
Текущая версия на 20:22, 30 мая 2013
Основные типы уравнений
- Уравнения баланса
- Определяющие уравнения
Определяющие уравнения являются целевым отражением исследуемых свойств среды, описывающим взаимодействие частиц. В зависимости от определяющих уравнений теории пластичности подразделяются на два класса:
- Феноменологические теории пластичности
- Физические теории пластичности
Феноменологические теории пластичности[править]
Основываются на описании явлений без изучения их причин
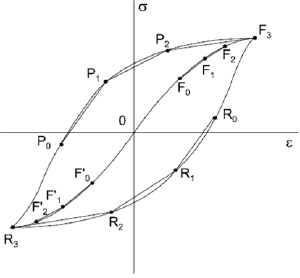
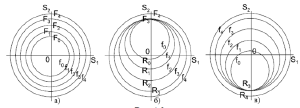
- Теория пластического течения
Используется критерий Мизеса или Треска для определения момента начала пластического течения. Рассматриваются три типа законов упрочнения: изотропный, кинематический, комбинированный. Данная теория позволяет с достаточной для прикладных задач МДТТ точностью описывать процессы при близких к простым нагружениях(деформирование по траекториям малой кривизны). На данный момент теория широко используется, вводятся многоповерхностные теории и варьируются законы упрочнения.
- Эндохронная теория пластичности
Используется понятие внутреннего времени. Описывает эффекты линейного и нелинейного упрочнения. Однако при сложных траекториях нагружения позволяет описать эффекты только качественно. В связи с возрастающим в последнее время интересом к зависимости пластических деформаций от скорости деформирования возникает вопрос о взаимосвязи внутреннего времени с реальным.
Физические теории пластичности[править]
Вводятся в рассмотрение механизмы пластического течения (в первую очередь дислокации).
- Модель Тейлора
Поликристалл представляет собой агрегат из большого числа хаотично ориентированных зерен. Поведение каждого из зерен описывается жесткопластической моделью. Деформации зерен осуществляются только кристаллографическим сдвигом.Рассматривается изотропный закон упрочнения. Деформации полагаются однородными в пределах макроскопического представительного объема. Активные системы скольжения определяются из условия минимальности суммарного сдвига. Модель достаточно точно описывает поведение поликристаллических тел, в связи с чемв настоящее время используются ее различные модификации, позволяющие решать возникающие при ее реализации проблемы. Однако эта модель приводит к неоднозначности решения задач и является относительно трудоемкой.
- Модель Бишопа-Хилла
В модели используется понятие поверхности текучести. Принимается ассоциированный закон пластического течения. Пренебрегаем упругими деформациями. Используется принцип максимума работы. Модель приводит к проблемам, аналогичным модели Тейлора.
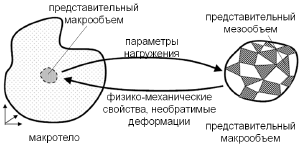
- Многоуровневые модели
В последнее время наиболее развивающийся класс моделей. С уровня реального тела спускаемся на уровень поликристалла, и далее вплоть до атомного уровня. Хотя в моделях этого типа максимально учитываются физические аспекты, на нижнем уровне необходимо зхамыкать модеть феноменологическими уравнениями, что также приводит к сложностям. Более того, возникают проблемы, связанные с вычислительной погрешностью и погрешностью согласования уровней.