Моделирование динамики толпы в областях со сложной геометрией — различия между версиями
Денис (обсуждение | вклад) |
Денис (обсуждение | вклад) |
||
| Строка 14: | Строка 14: | ||
Для описания взаимодействия частиц (людей) используется положительная часть потенциала Леннарда-Джонса – частицы отталкиваются друг от друга, но не притягиваются. | Для описания взаимодействия частиц (людей) используется положительная часть потенциала Леннарда-Джонса – частицы отталкиваются друг от друга, но не притягиваются. | ||
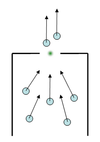
Чтобы смоделировать стремление людей попасть в определенную область – на моделирующей области задано векторное поле сил, устремляющее частицу к «выходу» | Чтобы смоделировать стремление людей попасть в определенную область – на моделирующей области задано векторное поле сил, устремляющее частицу к «выходу» | ||
| + | |||
| + | ---- | ||
[[Файл: MDC_prog_visual.png|150px|thumb|right|Графическая составляющая программы]] | [[Файл: MDC_prog_visual.png|150px|thumb|right|Графическая составляющая программы]] | ||
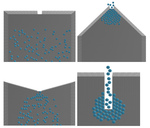
Для более наглядного отображения результатов моделирования разработаны средства визуализации, позволяющие отобразить достаточное количество частиц и требуемую геометрию области | Для более наглядного отображения результатов моделирования разработаны средства визуализации, позволяющие отобразить достаточное количество частиц и требуемую геометрию области | ||
| + | Для оценки ситуации измеряются две величины – время прохождения частиц через отверстие, и давление, возникающее в группе частиц. Требуется достичь минимального времени, однако при этом давление не должно превышать некоторого критического значения – чтобы максимально снизить риск травмирования людей в толпе. | ||
| + | |||
| + | Для расчета давления в системе, используется формула из главы «Техника моделирования» книги А. М. Кривцова «Деформирование и разрушение твердых тел с микроструктурой». | ||
| + | |||
| + | <math>\underline{\underline{\tau}} = -\frac{1}{2V}\sum_{\alpha}A_\alpha F_\alpha</math> | ||
| + | |||
| + | <math>p = -\frac{1}{d}tr(\underline{\underline{\tau}}) = -\frac{1}{2Vd}\sum_{\alpha}A_\alpha \cdot F_\alpha</math> | ||
[[MDCrowd_K1|Конфигурация с бортиками]] | [[MDCrowd_K1|Конфигурация с бортиками]] | ||
Версия 01:21, 7 апреля 2013
Введение
В работе исследуются способы более оптимальной организации движения людей, особенно в условиях паники – ведь в таком случае появляется большой риск получения людьми увечий вследствие увеличения «давления» в толпе.
Актуальность данной проблемы подтверждается, например, событиями в 2010 году в Дуйсбурге на фестивале «Love Parade», в ходе которого образовалась давка, в результате которой погиб 21 человек, и было ранено около 500 человек.
Цель
Цель работы – смоделировать и исследовать движение толпы при различных условиях, найти лучшие способы организации движения в таких местах, как проход в метрополитен, фойе театра, проход в концертный зал, и в других местах, предполагающий переход большого количества людей через некий узкий проём.
Реализация
Для моделирования данной задачи используется программа, написанная на языке Java с использованием библиотеки OpenGL. Для описания взаимодействия частиц (людей) используется положительная часть потенциала Леннарда-Джонса – частицы отталкиваются друг от друга, но не притягиваются. Чтобы смоделировать стремление людей попасть в определенную область – на моделирующей области задано векторное поле сил, устремляющее частицу к «выходу»
Для более наглядного отображения результатов моделирования разработаны средства визуализации, позволяющие отобразить достаточное количество частиц и требуемую геометрию области
Для оценки ситуации измеряются две величины – время прохождения частиц через отверстие, и давление, возникающее в группе частиц. Требуется достичь минимального времени, однако при этом давление не должно превышать некоторого критического значения – чтобы максимально снизить риск травмирования людей в толпе.
Для расчета давления в системе, используется формула из главы «Техника моделирования» книги А. М. Кривцова «Деформирование и разрушение твердых тел с микроструктурой».