Степанов Алексей. Курсовой проект по теоретической механике — различия между версиями

Версия 23:11, 25 июня 2012

Тема проекта

Описание колебаний плавающих тел.

Постановка задачи

Найти уравнение колебаний для следующих тел:
1) Шар
2) Параллелепипед

1. Вертикальные колебания
   
2. "Бортовая качка"
   

Решение

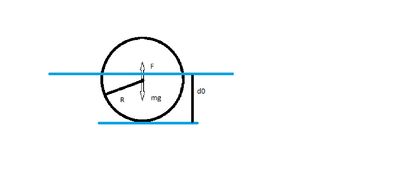
1) Шар

ПУР: [math]mg = \rho g V_0 = \frac{\pi \rho g} {3} d_0^2 (3R-d_0);[/math]
[math]d_o[/math] - начальная глубина погружения [math]\rho[/math] - плотность жидкости [math]R[/math] - радиус шара
Второй закон Ньютона примет вид:
[math]m \ddot x = -\frac{\pi \rho g} {3} d_0^3 + \pi \rho g d_0^2R - \frac{\pi \rho g} {3}(d_0+x)^2(3R-d_0-x)[/math]
После возведения в квадрат получаем:
[math]m \ddot x = -\frac{\pi \rho g} {3} d_0^3 + \pi \rho g d_0^2R - \frac{\pi \rho g} {3}(d_0^2 + 2 d_0x + x^2)(3R-d_0-x)[/math]
Проводим линеаризацию уравнения
[math]m \ddot x = -\frac{\pi \rho g} {3} d_0^3 + \pi \rho g d_0^2R - \frac{\pi \rho g} {3}(d_0^2 + 2 d_0x + o(x^2))(3R-d_0-x)[/math]
Раскроем скобки:
[math]m \ddot x = -\frac{\pi \rho g} {3} d_0^3 + \pi \rho g d_0^2R - \frac{\pi \rho g} {3}(3d_o^2R - d_0^3 + 6d_0Rx - 3d_0^2x)[/math]
В результате имеем:
[math]m \ddot x = \pi \rho g d_0(-2 R + d_0)x[/math];
Так как [math](-2 R + d_0) \lt 0[/math] формула имеет вид [math]m \ddot x + \pi \rho g d_0(2 R - d_0)x = 0[/math]
Остается проверить размерность величины [math]\omega^2 = \frac{\pi \rho g d_0(2 R - d_0)} {m} = \frac {1} {s^2}[/math]
Уравнение колебаний найдено.
2) Вертикальные колебания параллелепипеда

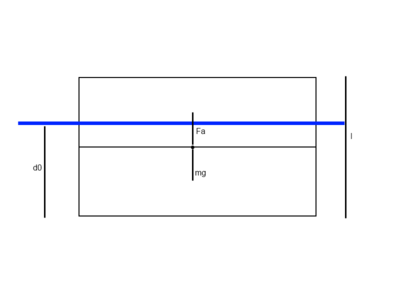
ПУР: [math]mg = \rho g V_0 = \rho g S d_o;[/math]
[math]d_o[/math] - начальная глубина погружения [math]\rho[/math] - плотность жидкости [math]S[/math] - площадь сечения
Второй закон Ньютона примет вид:
[math]m \ddot x = mg -\rho g S (d_o + x)[/math]
После сокращения:
[math]m \ddot x = -\rho g S x[/math]
Остается проверить размерность величины [math]\omega^2 = \frac{\rho g S} {m} = \frac {kg m^3} {s^2 m^3 kg} = \frac {1} {s^2}[/math]
Уравнение колебаний найдено.
2) Бортовая качка
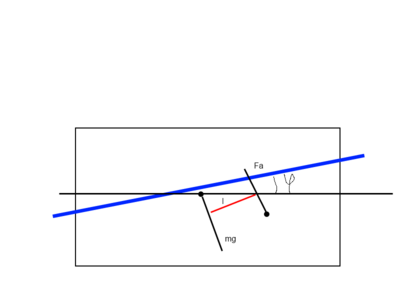Очевидно, что модуль силы Архимеда остается постоянным(так как постоянным остается объем погруженной части тела в силу симметрии тела). Меняется только точка приложения, что и создает момент силы Архимеда, вызывающий колебания. Тогда уравнения примут вид:
[math]\Theta_c \ddot \varphi = -F_a l \cos \varphi = -F_a l[/math]
[math]\Theta_c[/math] - момент инерции тела относительно центра масс [math]F_a[/math] - сила Архимеда [math]l[/math] - плечо силы Архимеда
[math]l = h \frac {h {\rm tg}\varphi} {6 d} = = h \frac {h \varphi} {6 d}[/math]
Так как тело плавает [math]F_a = mg[/math]
[math]\Theta_c \ddot \varphi = -\frac {mg h^2} {6 d} \varphi[/math]
Итоговое уравнение:
[math]\ddot \varphi + \frac {mg h^2} {6 d\Theta_c}\varphi = 0 [/math]

Обсуждение результатов и выводы

1) Можно заметить, что угловая частота колебаний шара имеет максимум в точке [math]d_0 = R[/math]
2) Интересно то, что [math]\frac{\rho g S} {m} = k \frac{g} {l}[/math], где l - полная высота параллелепипеда, а k - коэффициент, равный отношению жидкости тела к плотности тела
3)Пусть тело площадью сечения [math]10^{-2} m^2[/math] и массой [math]1 kg[/math] плавает в воде([math]\rho = 10^3 \frac{kg} {m^3}[/math]). Период вертикальных колебаний будет равен [math]T = 0.62 \quad c[/math]
Предположим, что это тело - куб [math]10 cm^3[/math]. Момент инерции куба относительно оси, проходящей через его центр масс, перпендикулярно поверхности [math]\Theta_c = \frac {m(2 a^2)} {12}[/math], где [math]a[/math] - длина стороны куба. Тогда [math]T = 0.62 c[/math]
4) Частоты колебаний параллелепипида оказываются схожими с частотой колебаний математического маятника при вертикальной качке и с частотой колебаний физического маятника при "бортовой качке".
Например, сравним [math]T = 2 \pi \sqrt{\frac{\Theta_c} {mgr}}[/math] и [math]T = 2 \pi \sqrt{\frac{\Theta_c} {m g \frac{h} {2}} \frac {3d} {h}}[/math], [math]r[/math] - расстояние от точки подвеса до центра тяжести физ. маятника, а[math]d[/math] и [math]h[/math] высота и длина параллелепипеда соответственно.

Ссылки по теме

Архимед

См. также

• Справочная информация
• Список курсовых проектов
• Кафедра "Теоретическая механика"
• Степанов Алексей