Краморов Данил. Курсовой проект по теоретической механике — различия между версиями

Версия 18:06, 26 мая 2012

Тема проекта

Колебания шарика в вертикальном воздушном потоке

Постановка задачи

Тело - в данном эксперименте шарик для настольного тенниса - помещается на край вертикального воздушного потока (создается феном). Подчиняясь закону Бернулли, шарик будет пытаться стабилизироваться в центре потока, совершая колебания. Требуется найти уравнение колебаний шарика. Рассматриваются только горизонтальные колебания внутри потока.

Параметры системы:

[math] d = 4*10^{-2}[/math]м (диаметр потока)
[math] \rho = 0.125 [/math]кг/м^3 (массовая плотность воздуха)
[math] A = 12,56*10{-4} [/math] м^2 (площадь поперечного сечения шара)
[math] Cl = 0.5 [/math] (коэффициент подъемной силы)

Решение

Рассмотрим горизонтальную составляющую второго закона Ньютона для данного тела. В этом направление на шарик действуют только две силы: подъемная сила (объясняемая эффектом Магнуса) и сила аэродинамического сопротивления.

[math]m \ddot x = \frac{1} {2} \rho \upsilon^2 ACl - A \dot x^2;[/math]

[math] \rho[/math] — плотность жидкости
[math] \upsilon[/math] — скорость шара
A — поперечная площадь шара
Cl — коэффициент подъёмной силы

Распределение Гаусса

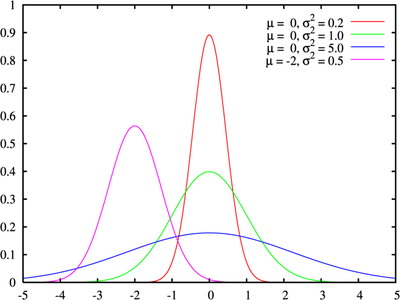
Задача сводится к нахождению функции, описывающей скорость шара в вертикальном воздушном потоке. Найти требуемую функцию можно разными способами. Максимальная скорость (5.6 м/с, расчет был произведен в эксперименте, изучающем закон Бернулли) будет достигаться в центре потока. По краям же скорость будет меньшей. Следовательно в грубом приближение функция скорости будет повторять функцию распределения вероятностей (распределение Гаусса). Функция плотности распределения имеет вид:

[math]f(x)= \frac{1} {\sigma \sqrt{2\pi}} e^{-\frac{(x- \mu)^2} {\sigma^2}}[/math]

[math] \mu[/math] - коэффициент сдвига (вещественное число)
[math] \sigma[/math] - коэффициент масштаба (вещественный, строго положительный)

Представляя данную функцию функцией скорости, получаем зависимость от местоположения в потоке.
[math] \mu[/math] = d/2, [math] \sigma[/math] = d/6, где d - диаметр потока.

[math] \upsilon(x)= \frac{1} {\frac{d} {6} \sqrt{2\pi}} e^{-\frac{(x- \frac{d} {2})^2} {({\frac{d} {6}})^2}}[/math]
[math] \upsilon(x)= \frac{6} {d \sqrt{2\pi}} e^{-\frac{9(2x- d)^2} {d^2}}[/math]

Общая формула будет иметь вид:

[math]m \ddot x = \frac{k} {\pi d^2} e^{-\frac{(2x- d)^2} {d^2}} - A \dot x^2;[/math]

где [math] A = 12,56*10^{-4} [/math], [math] k = 7*10^{-4} [/math];

Обсуждение результатов и выводы

Аналитический расчет подтвердил экспериментальную оценку. Окончательное уравнение показало, что тело в вертикальном воздушном потоке совершает затухающие колебания. Также можно отметить, что колебания оказались очень малы. Шарик практически моментально стабилизируется в потоке. Что касается вертикальных колебаний, то они зависят от перепадов напряжения в сети и носят довольно случайный характер. Посредством пакета matlab были построены графики скорости, ускорения и движения тела в потоке.

Ссылки по теме

См. также

• Справочная информация
• Список курсовых проектов
• Кафедра "Теоретическая механика"
• Краморов Данил