Дзенушко Дайнис. Курсовой проект по теоретической механике — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Решение)
(→‎Решение)
Строка 18: Строка 18:
 
== Решение ==
 
== Решение ==
 
'''Определимся с подходом к решению:''' Задачу будем решать при помощи уравнения Лагранжа имеющего следующий вид:<br>
 
'''Определимся с подходом к решению:''' Задачу будем решать при помощи уравнения Лагранжа имеющего следующий вид:<br>
−
<math>\frac{d}{dt}\frac{\partial T}{\partial \dot{q}_i}-\frac{\partial T}{\partial q_i} = -\frac{\partial \Pi}{\partial q_i}</math><br>
+
<math>\frac{d}{dt}\frac{\partial T}{\partial \dot{q}_i}-\frac{\partial T}{\partial q_i} = -\frac{\partial \Pi}{\partial q_i}+Q_i</math><br>
 
*<math>T</math> - Кинетическая энергия системы <br>
 
*<math>T</math> - Кинетическая энергия системы <br>
 
*<math>\Pi</math> - Потенциальная энергия системы<br>
 
*<math>\Pi</math> - Потенциальная энергия системы<br>
 
*<math>q_i</math> - Обобщенные координаты<br>
 
*<math>q_i</math> - Обобщенные координаты<br>
 
*<math>\dot{q}_i</math> - Обобщенные скорости<br>
 
*<math>\dot{q}_i</math> - Обобщенные скорости<br>
 +
*<math>Q_i</math> - Обобщенные непотенциальные силы<br>
 +
<br>
 +
'''Выберем обобщенные координаты:''' в качестве обобщенных координат возьмем углы <math>\phi</math> и <math>\psi</math> <br>
 +
*В нашем случае отсутствуют обощенные силы, соответствующие непотенциальным взаимодействиям.<br>
  
 
== Обсуждение результатов и выводы ==
 
== Обсуждение результатов и выводы ==

Версия 13:46, 20 мая 2012

Тема проекта

Описание движения двойного маятника

Постановка задачи

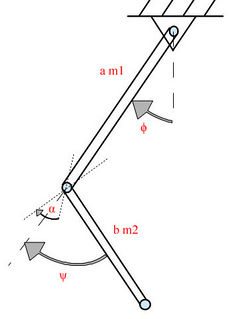
Стержень прикреплен к потолку посредством циллиндрического шарнира. Cнизу к этому стержню прикреплен второй также посредством циллиндрического шарнира таким образом что когда маятник вытянут вдоль вертикали, обе оси вращения шарниров расположены в горизонтальной плоскости а угол между ними составляет [math]\alpha[/math]. Диссипативные силы не учитываются.
Параметры системы:

  1. Тензоры инерции первого и второго стержней равны [math]\underline{\underline{\Theta}}_1[/math] и [math]\underline{\underline{\Theta}}_2[/math] соответственно.
  2. Длины стержней равны a и b, их массы [math]m_1[/math] и [math]m_2[/math] соответственно первому и второму стержням.
  3. Угол между осями вращения шарниров равен [math]\alpha[/math]
  • [math]\phi[/math] - угол между первым стержнем и вертикалью
  • [math]\psi[/math] - угол между осью первого стержня и вторым стержнем т.е. угол во втором шарнире относительно вытянутого положения
  • 2 oscillator.jpg


Задача:

  • Найти уравнение движения системы

Решение

Определимся с подходом к решению: Задачу будем решать при помощи уравнения Лагранжа имеющего следующий вид:
[math]\frac{d}{dt}\frac{\partial T}{\partial \dot{q}_i}-\frac{\partial T}{\partial q_i} = -\frac{\partial \Pi}{\partial q_i}+Q_i[/math]

  • [math]T[/math] - Кинетическая энергия системы
  • [math]\Pi[/math] - Потенциальная энергия системы
  • [math]q_i[/math] - Обобщенные координаты
  • [math]\dot{q}_i[/math] - Обобщенные скорости
  • [math]Q_i[/math] - Обобщенные непотенциальные силы


Выберем обобщенные координаты: в качестве обобщенных координат возьмем углы [math]\phi[/math] и [math]\psi[/math]

  • В нашем случае отсутствуют обощенные силы, соответствующие непотенциальным взаимодействиям.

Обсуждение результатов и выводы

Ссылки по теме

См. также

Источник — «http://tm.spbstu.ru/?title=Дзенушко_Дайнис._Курсовой_проект_по_теоретической_механике&oldid=11901»